RND指令执行出错的原因分析
|
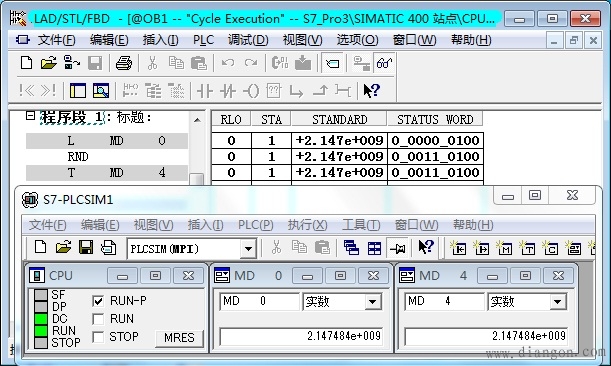
网友ktissot在用下面3条指令将浮点数转换为双整数时,发现了一个神秘的现象。 L MD0
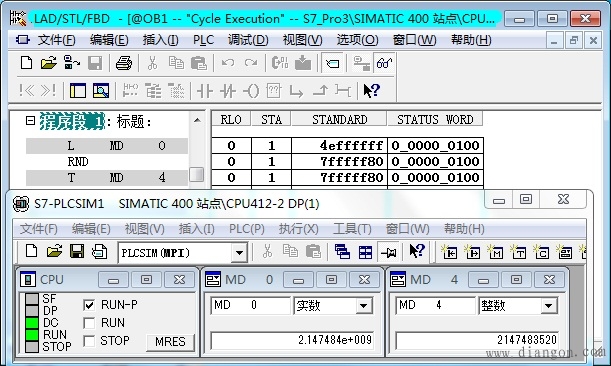
2.转换成功的情况 小于16777215.0左右转换结果完全正确。转换成功时OV和OS为0。 小于2147483584.0到16777215.0这一段可以转换,但是转换有误差。 接近2147483584.0时,最大误差为64。 大于2147483456.0 ~ 2147483584.0时(区间范围为128.0),转换后得到的双整数均为2147483520(16#7FFF FF80,见下图)。转换结果2147483520是区间中点的值,(2147483456 2147483584)/2= 2147483520。 大于2147483328.0 ~ 2147483456.0时,转换后得到的双整数均为2147483392(16#7FFF FF00)。 大于2147483200.0 ~ 2147483328.0时,转换后得到的双整数均为2147483264(16#7FFF FE80)。 经过分析,我已经找到了上述现象的原因,结果暂不公布,希望有兴趣的网友一起来分析一下,共享解决问题的快乐。
3.转换结果分析 大于2147483456.0 ~ 2147483584.0时转换后得到2147483520(16#7FFF FF80)。 大于2147483328.0 ~ 2147483456.0时转换后得到2147483392(16#7FFF FF00)。 大于2147483200.0 ~ 2147483328.0时转换后得到2147483264(16#7FFF FE80)。 上述3个区间内部的间隔为128.0,转换结果为区间的中点(2147483456 2147483584)/2= 2147483520。 所以这种转换并不精确,最大误差为128/2=64。 浮点数转换为双整数的转换误差的根本原因是32位浮点数和32位双整数的有效位数的差异造成的。 浮点数由一位符号位、8位指数和尾数的小数部分(23位)组成。尾数的位数决定了浮点数的精度。尾数的整数部分为1,小数部分为23位,所以尾数的有效数字为24位。 双整数除去一位符号位,其有效位数为31位,因此浮点数的有效位数比双整数少7位。 2147483456.0 ~ 2147483584.0相差128.0,它们对应的整数为31位有效数字,这些浮点数输入plc后,因为浮点数的有效位数只有24位,它们的尾数相同,对应的十六进制表示的浮点数均为16#4EFF FFFF,或2.17484e 009(注意有效尾数为十进制7位,而不是对应的整数的10位)。所以转换为双整数后均为2147483520。 ktissot网友说:“这就像看一片湖水一样,你可以看到水和浪花,但是绝对看不到水分子。”由于有效位数较小,浮点数不能分辨“水分子”2147483457.0 ~ 2147483584.0,我们只能看到“浪花”2147483520(16#7FFF FF80)。 如果浮点数较小,例如小于16777215(16#FF FFFF),整数部分只有24位,转换后就没有上述的误差了。在此基础上增大,整数部分的位数越大,误差越大。 因为有效位数相差7位,在接近双整数最大值的区段,浮点数的尾数相差一个数时,转换为双整数后,相差128。2的7次方等于128。 4.高端转换出错的原因分析 为什么最高端大于2147483584.0的数不能正确地转换呢?请注意小于2147483648.0到大于2147483584.0这段范围刚好是64.0(128.0的一半)。RND指令在转换时将这段范围的尾数四舍五入后,尾数的最低位加1,相当于转换后的整数加128(16#80),由上述的16#7FFF FF80(2147483520)加16#80后变为16#8000 0000,超出了双整数整数的允许范围,产生了溢出,所以转换出错。 |