流入电流互感器CT一次侧的电流信号是50 Hz的工频信号,如果电流互感器发生饱和,则二次电流会出现波形缺损和畸变。防止CT饱和引起保护的误动一直是电流差动保护的核心问题。但对于输电线路的距离保护,通常认为在线路出口附近故障时CT才会发生饱和,线路末端故障时不会引起饱和,并且由于CT饱和后二次测量电流减小,测量阻抗增大,不会发生误动的问题。随着电力系统的发展,系统短路容量不断增大、短线增多,线路末端故障时CT饱和的现象已引起人们的注意。事实上线路电流差动保护中均采取了防止CT饱和引起误动的措施。数字式保护都是采用一定的算法来计算电压和电流,在CT饱和后,距离保护是否会超越有必要进行深入研究。 1距离保护算法简介 距离保护算法是在得到基频电压向量和基频电流向量的基础上,取两者的比值计算出保护安装处到故障点之间的故障阻抗,即Z=UI,然后根据测量阻抗判断保护是否动作。为了消除故障暂态过程中非周期分量和高次谐波分量对测量阻抗的影响,目前广泛采用傅氏算法计算电压和电流相量,在实际应用中常常采用下面三种算法: 1) 全波傅氏算法。基频向量的实部和虚部分别为:
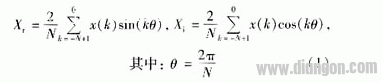
2) 加差分的全波傅氏算法。采用差分是为了进一步抑制信号中衰减非周期分量的影响。 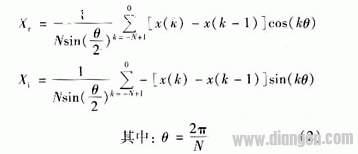
3) 加差分的半波傅氏算法。
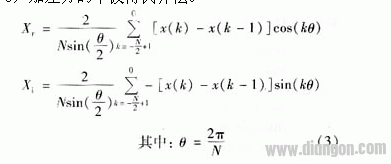
本文以上面三种算法为对象,研究CT饱和时距离保护的超越情况。
2仿真计算
由于线路末端故障时发生CT饱和的现象通常只在短线中发生,故在仿真计算中采用500 kV、40 km的短线模型。输电线路的参数为:正序参数所示。
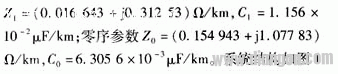
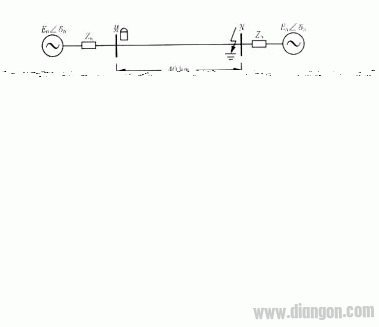
CT采用LCLWDG-220型,其变比为1200/5,励磁曲线的数据如表1所示,其模型如图2所示,其中采用98号非线性电感元件来模拟该CT的饱和励磁曲线。
仿真数据由电磁暂态仿真程序(ATP)产生,保护安装处的电压和电流取的是分别经过电压互感器和电流互感器变换后的二次侧数据,并都经过一个截止频率为300 Hz的数字低通滤波器进行前置滤波。采样频率为1 KHz(20点/周波)。故障发生在MN线路末端,故障类型为单相接地故障和相间故障。为了研究在不同的CT饱和程度下该算法的估计性能,CT二次侧的负载分别设为3.5 Ω、4.3 Ω、5.3 Ω、6 Ω、7 Ω。由于衰减直流分量的大小是影响CT饱和的一个重要因素,而衰减非周期分量的大小与短路水平和故障的发生时刻(合闸角)有关。所以在仿真中,故障合闸角分别取-45°、0°、30°、60°、90°,这样比较全面的反映衰减非周期分量的大小。
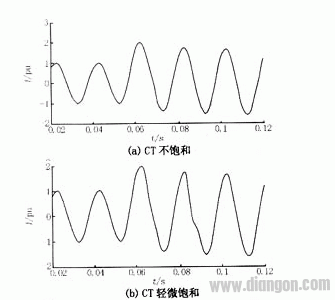
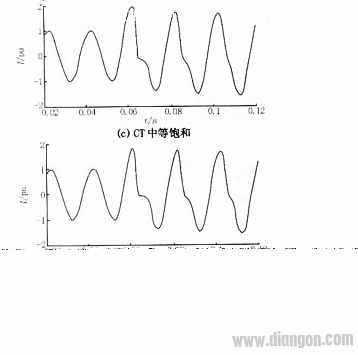
图3给出了CT在不饱和以及各种饱和程度下的电流信号波形,其中电流已归算到标幺值。轻微饱和、中等饱和和严重饱和是对应合闸角为0°,CT二次侧负载分别为3.5 Ω、5.3 Ω、7 Ω情况下CT的饱和程度。
3仿真结果分析
下面的仿真分析均以线路阻抗ZL=(0.666 j12.501) Ω作为基准值,测量阻抗已经归算成标幺值。从仿真结果来看,傅氏算法在合闸角90°为附近故障,也就是对称性饱和时保护不会发生超越的现象,只有在合闸角为0°左右时电流信号包含的非周期分量最大,因此CT饱和的程度比较严重,引起超越的可能性也最大。下面对各种算法进行详细分析。
3.1CT饱和对全波傅氏算法的影响
为了更好地说明CT饱和对算法的影响,对全波傅氏算法估计的测量阻抗在CT不同饱和情况下的暂态超越情况做了一个统计,详见表2。为了方便解释,先定义电抗测量误差EX=(XL-X)/XL,XL为线路电抗,为测量阻抗的电抗分量。超越的开始时刻指的是以故障时刻为起始点(0 ms),EX开始大于0的时刻。当EX大于5%时称为超越5%。类似的,EX大于10%称为超越10%,大于20%称为超越20%。
在一个周波内,CT只是部分时间发生饱和,故测量阻抗随着数据窗的移动是变化的。图4表示单相接地故障时,在CT不同饱和程度下全波傅氏算法估计的测量阻抗随着数据窗移动的轨迹变化图。其中,阻抗点旁边的数字表示从故障时刻开始数据窗填满(即故障发生20 ms)后向后移动的点数。
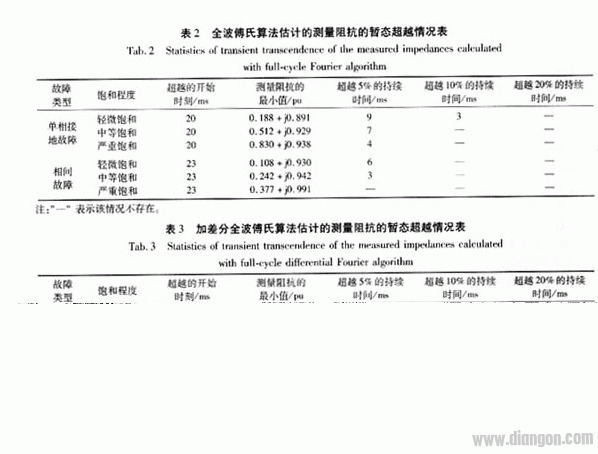
 从表2和图4可以看到,无论是单相接地故障还是相间故障,傅氏算法估计的测量阻抗都是在CT发生轻微饱和时最容易引起超越。随着饱和程度的加深,最小测量阻抗的电阻分量和电抗分量都增大,超越的时间缩短,并且超越的程度也在减小,控制在5%以内,在发生严重饱和时相间故障就不存在超越问题了。 从表2和图4可以看到,无论是单相接地故障还是相间故障,傅氏算法估计的测量阻抗都是在CT发生轻微饱和时最容易引起超越。随着饱和程度的加深,最小测量阻抗的电阻分量和电抗分量都增大,超越的时间缩短,并且超越的程度也在减小,控制在5%以内,在发生严重饱和时相间故障就不存在超越问题了。
3.2CT饱和对加差分的全波傅氏算法的影响
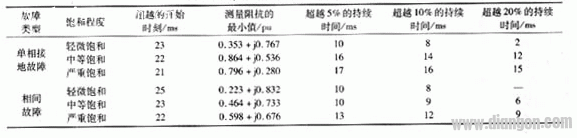
加差分全波傅氏算法估计的测量阻抗暂态超越情况详见表3。
单相接地故障时,利用该算法得到的测量阻抗轨迹变化图见图5。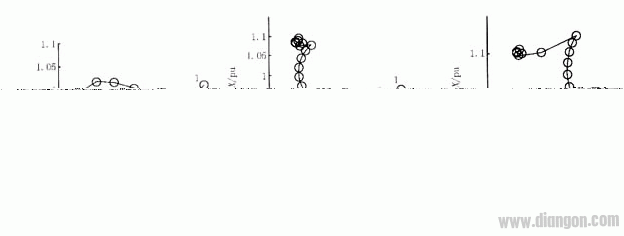
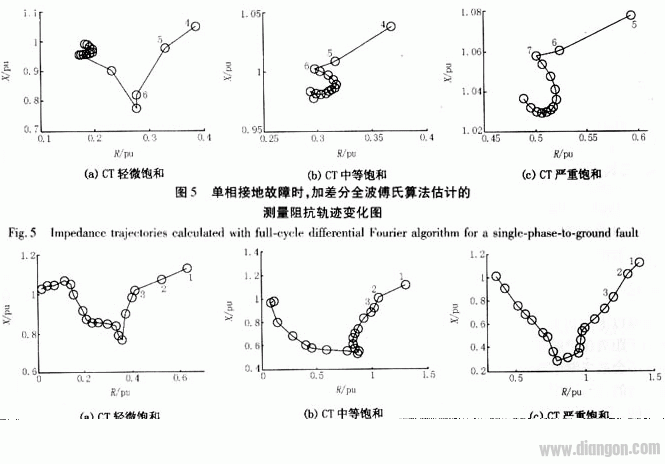 
从图5(a)可以看到,单相接地故障时,在移动数据窗过程中测量阻抗会出现电抗分量突然变得很小的情况,产生这种跳变的原因是采用了差分的方法。由于电抗分量的跳变,使得测量阻抗超越的程度比较大,超过了20%,从而使测量阻抗有可能进入保护动作区。从仿真结果看,电抗跳变的情况一般是在CT饱和程度比较轻的时候,当饱和程度加重时,在数据窗的移动过程中测量到的最小阻抗的电抗分量不断增大,超越的可能性越来越小。在中度饱和时虽然仍有超越的可能,但是程度很轻,不超过5%。而当饱和严重时,电抗分量已经大于1.0 pu,显然不存在超越的情况。
对相间故障,当CT饱和轻微时虽然也存在测量阻抗的电抗分量减小的情况,但是由于减小的幅度较小,所以超越的程度相应的也比较轻。当饱和程度加重时,最小测量阻抗的变化和单相接地故障类似。
3.3CT饱和对加差分的半波傅氏算法的影响
类似的,表4给出了加差分傅氏算法估计的测量阻抗暂态超越情况。
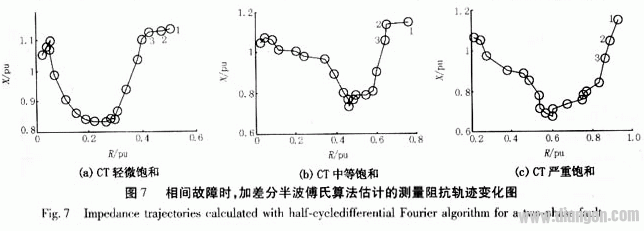
图6和图7分别给出了在单相接地故障和相间故障情况,利用该算法估计的测量阻抗在CT不同饱和程度下的轨迹变化图。
显然,CT饱和对加差分半波傅氏算法的影响很大,在不同的饱和程度下均发生了暂态超越行为。随着CT饱和程度的加深,移动数据窗过程中的最小测量阻抗的电抗分量不断减小,说明超越行为随着饱和程度的加深而变得严重。CT饱和程度越重,发生超越的时刻越早,超越持续的时间越长,超越的幅度也越大。饱和轻微时超越5%的时间就达到半个周期之长,饱和严重时甚至将近一个周期,可见CT饱和对算法影响之深。其中单相接地故障的暂态超越情况要比相间故障严重些,即使在轻微饱和时,都存在超越幅度超过20%的阻抗点,很容易会导致继电器的误动。 请登陆:输配电设备网 浏览更多信息
4结论
根据以上的仿真分析可以看到,在CT饱和情况下用于距离保护的傅氏算法并不象我们直观认为的那样不会造成继电器的误动。事实上它是会产生超越行为的,但是对不同的傅氏算法,超越的程度又不太相同,下面是上述三种傅氏算法暂态超越情况的小结:
1) 全波傅氏算法在CT饱和轻微时超越的情况最严重,随着饱和的加重,超越程度变轻,持续的时间也缩短。
2) 加差分全波傅氏算法只在CT轻微饱和时才会产生超越行为。
3) 加差分半波傅氏算法在CT不同饱和程度下都存在超越,并且饱和程度越深,超越开始的时刻越早,持续的时间越长,超越的幅度越大。
由于在CT饱和时,上述三种用于数字式距离保护的傅氏算法都存在不同程度上的超越行为,所以在采用时必须采取一定的措施来防止CT饱和引起的超越,从而避免继电器造成不必要的误动。
| 
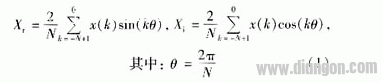
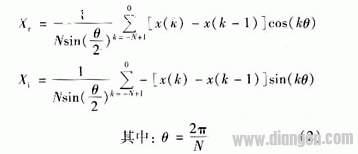
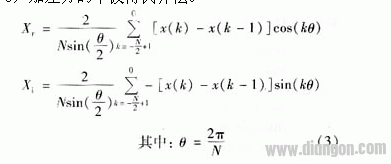
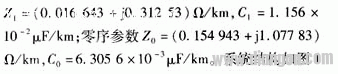



 从表2和图4可以看到,无论是单相接地故障还是相间故障,傅氏算法估计的测量阻抗都是在CT发生轻微饱和时最容易引起超越。随着饱和程度的加深,最小测量阻抗的电阻分量和电抗分量都增大,超越的时间缩短,并且超越的程度也在减小,控制在5%以内,在发生严重饱和时相间故障就不存在超越问题了。
从表2和图4可以看到,无论是单相接地故障还是相间故障,傅氏算法估计的测量阻抗都是在CT发生轻微饱和时最容易引起超越。随着饱和程度的加深,最小测量阻抗的电阻分量和电抗分量都增大,超越的时间缩短,并且超越的程度也在减小,控制在5%以内,在发生严重饱和时相间故障就不存在超越问题了。