西门子PID调节应用及技巧探讨

要用好PID调节，搞清楚PID的计算公式和PID参数的意义是很有必要的。下面是PID的公式：



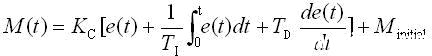
式中误差信号e(t) = SP(t) – PV(t)，M(t)是PID控制器的输出值，Kc是控制器的增益（比例系数），Ti和Td分别是积分时间和微分时间，Minitial是M(t)的初始值，实际上是积分的初始值。
PID公式的前3项分别与误差、误差的积分和误差的导数成正比。
微分、积分是高等数学的概念，建议没有学过高等数学的网友至少要搞清楚微分和积分的几何意义，这对深入理解PID参数的意义有很大的帮助。
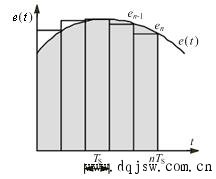
积分对应于下图中误差曲线e(t) 与坐标轴包围的面积（图中的灰色部分）。PID程序是周期性执行的，执行PID程序的时间间隔为Ts（即PID控制的采样周期）。我们只能使用连续的误差曲线上间隔时间为Ts的一些离散的点的值来计算积分，因此不可能计算出准确的积分值，只能对积分作近似计算。
一般用下图中的矩形面积之和来近似精确积分。当Ts较小时，积分的误差不大。



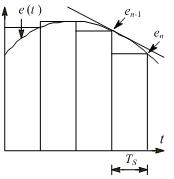
在误差曲线e(t)上作一条切线（见下图），该切线与x轴正方向的夹角α的正切值tgα即为该点处误差的一阶导数de(t)/dt。PID控制器输出表达式中的导数用下式来近似：
de(t)/ dt ≈ Δe(t)/Δt = [e(n) - e(n-1)]/Ts，式中e(n)是第n次采样时的误差值，e(n-1)是第n-1次采样时的误差值。


PID调节是目前应用最广泛调节控制规律，P比例、I积分、D微分控制，简称PID控制。
比例控制是一种最简单的控制方式。比例作用大，可以加快调节，减少误差，但是过大的比例，使系统的稳定性下降，甚至造成系统的不稳定。
积分调节可以使系统消除稳态误差。系统如果在进入稳态后存在稳态误差，就必须引入“积分项”。比例 积分(PI)控制可以使系统在进入稳态后无稳态误差。
微分作用能产生超前的控制作用，在偏差还没有形成之前，已被微分调节作用消除。因此，可以改善系统的动态性能。。对有较大惯性或滞后的被控对象，比例 微分（PD）控制能改善系统在调节过程中的动态特性。
这是摘录的一个PID参数调整的口诀，以供大家学习参考：
参数整定找最佳，从小到大顺序查
先是比例后积分，最后再把微分加
曲线振荡很频繁，比例度盘要放大
曲线漂浮绕大湾，比例度盘往小扳
曲线偏离回复慢，积分时间往下降
曲线波动周期长，积分时间再加长
曲线振荡频率快，先把微分降下来
动差大来波动慢。微分时间应加长
理想曲线两个波，前高后低4比1
一看二调多分析，调节质量不会低。
这个顺口溜流传甚广，我觉得可操作性很低（也可能是我的悟性不够），我有很多疑问：
“从小到大顺序查“，查什么？
一定要”先是比例后积分“吗？直接用PI不好吗？
“曲线振荡很频繁”，是指振荡频率高还是振荡次数多？
什么是”比例度盘“？
”曲线漂浮绕大湾“什么意思？是指超调量大吗？还是上升缓慢？
”曲线波动周期长“的周期是震荡周期吗？还是过度过程时间长？
振荡频率和微分关系大吗？微分的主要作用是什么？
“理想曲线两个波”，一个波是180度还是360度？两个波是理想曲线，下图的PV曲线理不理想？


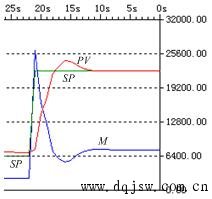
我用过S7-200和S7-200 SMART的PID调节控制面板和PID参数自整定功能，被控制对象采用我编写的子程序来模拟。被控对象的参数如下：增益为3.0，两个惯性环节的时间常数为5s和2s。
下面是自整定之前的曲线，超调量太大：



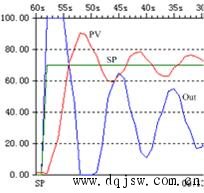
下面是整定过程的曲线：



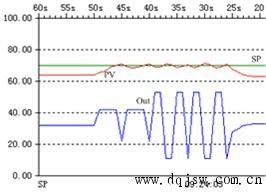
下面是整定得到的参数的曲线：



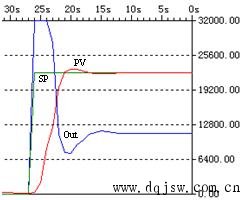
下面是另一组整定前的参数的曲线，过程变量PV曲线上升太慢：



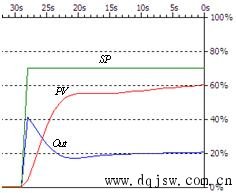
虽然整定前两组PID参数相差很远，两次整定后得到PID参数差不多，使用整定得到的PID参数的曲线形状也差不多。
我觉得西门子的PID参数自整定是很好用的。
要用好PID调节，搞清楚PID的计算公式和PID参数的意义是很有必要的。下面是PID的公式：



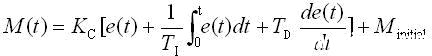
式中误差信号e(t) = SP(t) – PV(t)，M(t)是PID控制器的输出值，Kc是控制器的增益（比例系数），Ti和Td分别是积分时间和微分时间，Minitial是M(t)的初始值，实际上是积分的初始值。
PID公式的前3项分别与误差、误差的积分和误差的导数成正比。
微分、积分是高等数学的概念，建议没有学过高等数学的网友至少要搞清楚微分和积分的几何意义，这对深入理解PID参数的意义有很大的帮助。
积分对应于下图中误差曲线e(t) 与坐标轴包围的面积（图中的灰色部分）。PID程序是周期性执行的，执行PID程序的时间间隔为Ts（即PID控制的采样周期）。我们只能使用连续的误差曲线上间隔时间为Ts的一些离散的点的值来计算积分，因此不可能计算出准确的积分值，只能对积分作近似计算。
一般用下图中的矩形面积之和来近似精确积分。当Ts较小时，积分的误差不大。



在误差曲线e(t)上作一条切线（见下图），该切线与x轴正方向的夹角α的正切值tgα即为该点处误差的一阶导数de(t)/dt。PID控制器输出表达式中的导数用下式来近似：
de(t)/ dt ≈ Δe(t)/Δt = [e(n) - e(n-1)]/Ts，式中e(n)是第n次采样时的误差值，e(n-1)是第n-1次采样时的误差值。


1.模糊控制的关键点在于总结大量的实践数据，然后做成黑匣子，看似神秘，实际都是经验参数！
2.模糊控制得到的数据是基于控制设备性能不变的情况下，是较为准确的。一旦使用时间长了，性能有所下降，这些经验参数往往就会有很大的偏颇了。
3.即使是同样型号的不同设备，其所处于的工艺环境，工艺流程，工艺特性的不同，其性能也会有差别，因此不能做到模糊控制中同一数据的重复性使用。
4.模糊控制的理念是很好的，最起码是超前控制，但就目前而言，其实用性，动态性还是不如传统的PID。
5.传统PID是滞后控制，在目前的大多数工艺环境下，还是可以满足控制的需求的。
6.基于传统PID的特点，也延展了不同的控制方式，如串级调节，三冲量调节，分程调节，步进式等等。#p#分页标题#e#
7.个人觉得：随着电子，网络，计算机的飞速发展，传统PID的滞后也会改善的更好，其动态调节特性是模糊控制所不能比拟的。
搞清楚PID参数的物理意义，和PID参数与闭环系统性能指标的关系，对于指导我们调节PID至关重要。
PID的控制原理可以用人对炉温的手动控制来理解。首先看看比例部分的作用。
搞清楚PID参数的物理意义，和PID参数与闭环系统性能指标的关系，对于指导我们调节PID至关重要。首先看看比例部分的作用。
PID的控制原理可以用人对炉温的手动控制来理解。操作人员用眼睛读取数字仪表检测到的炉温的测量值，并与炉温的设定值比较，得到温度的误差值。用手操作电位器，调节加热的电流，使炉温保持在设定值附近。
操作人员知道使炉温稳定在设定值时电位器的位置（我们将它称为位置L），并根据当时的温度误差值调整电位器的转角。炉温小于设定值时，在位置L的基础上顺时针增大电位器的转角，以增大加热的电流；炉温大于设定值时，在位置L的基础上反时针减小电位器的转角，以减小加热的电流。令调节后的电位器转角与位置L的差值与误差成正比，误差绝对值越大，调节的角度越大。上述控制策略就是比例控制。
闭环中存在着各种各样的延迟作用。调节电位器转角后，到温度上升到新的转角对应的稳态值时有较大的延迟。由于延迟因素的存在，调节电位器转角后不能马上看到调节的效果，因此闭环控制系统调节困难的主要原因是系统中的延迟作用。
如果增益太小，调节的力度不够，使温度的变化缓慢，调节时间过长。如果增益过大，调节力度太强，造成调节过头，可能使温度忽高忽低，来回震荡。
如果闭环系统没有积分作用，单纯的比例控制有稳态误差，稳态误差与增益成反比。增益越大，稳态误差越小，但是会使超调量增大，振荡次数增加，甚至会使闭环系统不稳定。因此单纯的比例控制很难兼顾动态性能和静态性能。