步进电动机磁阻电动机静态特性转矩有限无法数值计算优化设计

步进电动机的设计和优化设计中最重要的是性能指标的预测，但是由于步进电动机的结构和运行条件特殊，人们在计算过程中往往要作某些假设，例如忽略磁路的饱和或是假定铁心部分的磁压降与转子位置无关等，以求得到简化，这自然会给计算结果带来一定的误差。为了充分考虑电机磁路的饱和对其性能的影响，本文将以样机BF36型磁阻式步进电动机为例，采用有限元数值解法，并借助网格自动剖分技术，对整个电机的求解区域进行磁场分析，求得电机磁场的磁共能，进而计算出电机的静态转矩。磁阻式步进电动机的定、转子齿形尺寸的不同，将影响电机磁路的磁导和电机磁场，从而影响电机的性能。

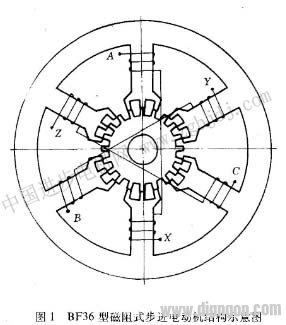
BF36型三相磁阻式步进电动机的结构如图1所示，定子上共有6个磁极，每极上有3个矩形齿，辖子上有Zr=20个均匀分布的矩形齿，定转子齿矩卢18度。电机的U_N= 24V，L_N= 0.15A，可以单相通电，也可以双相通电运行。

用有、限元数值解法计算磁阻式步进电动机的静转矩。可直接利用电机磁场的磁共能计算电磁转矩的公式[1]。

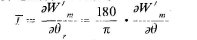式中θr一转子的角位移，radθ一转子的角位移，

为了算出电机的静态转矩特性，即矩角特性，就必须研究电机定子磁极线圈在不同电流下，以及转子相对定子有不同位置时的磁场分布情况。由于在齿距t范围内，在 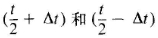的位置电机磁场对称，故只需研究半个齿距，即9度范围内各个位置的磁场情况即可。

设定转子齿中心线对齐时θ=0，根据电机的结构、 通电方式和磁场对称性，可选定半个电机的空间作为电机磁场的求解区域，图2示出这时求解区的网格剖分。

在某一θ值下磁极线圈通入电流后，经二维磁场的有限元计算[2]可得出此时求解区域内部节点的矢量磁位A值、各单元的磁通密度以及绘出求解区的磁力线分布。图3展示了θ=1度时，A、B两相同时通电的磁力线分布，再经后处理的计算，便可求得通电的磁极线圈所匝链的总磁链ψ。然后，改变电流的数值，再计算该θ位置的磁场和磁极线圈匝链的总磁链新值。这样，重复多次计算后便可得到一组不同的电流及其所产生的磁极线圈磁链，即得出在此转子位置θ下电机的电流与线圈磁链之间的关系ψ=f(I).

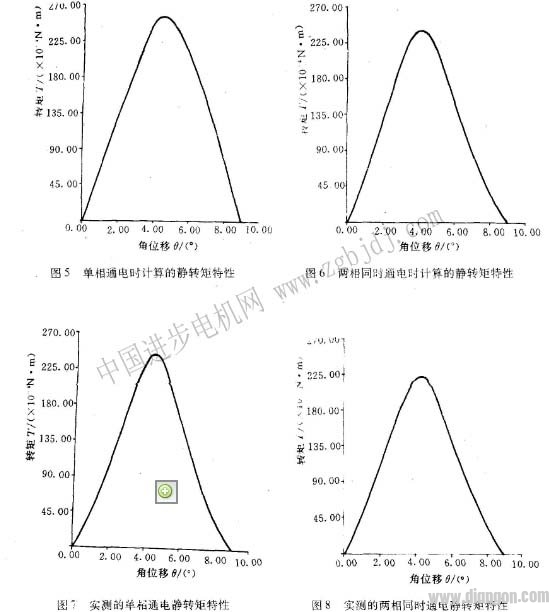
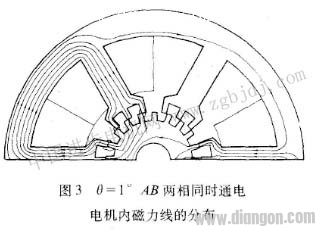如果转子在空间从θ=0起按顺时针方向每转过1度，再重复上述计算，直至θ=9度止（这在有限元数值分析中借助网格自动剖分技术后是容易实现的)，从而得出电机在所有10个定、转子相对位置的磁链与电流间的关系。图4是A相绕组通电状态下θ=0和θ=1度时电机的ψ=f(I)关系曲线。从而可用Simpson积分法‘3’分别求出在某一电流下各个θ位置的磁共能遍Wm，例如I= I_N=0.15A，θ=0时的磁共能值就是曲边形oaco的面积，θ=1度时的磁共能则为曲边形obco的面积。重复上述步骤，便可求出在此电流下θ=0.1度.2度……9度时所对应的10个电规的磁共能，即有Wm对应于0的10组对应值。然后，再用三次样条插值函数的微分公式(4)就能求得磁共能Wm。对θ导数，并根据式(I)即可得出步进电动机的静转矩特性曲线T=f(θ)。图5和图6表示该电机在额定电流下单相通电和两相同时通电时计算所得的静转矩特性。图7和图8则分别表示所对应的实测结果。两者相比较，最大静转矩的误差在单相通电时是百分之5 .41，两相同时通电时为百分之7.34。

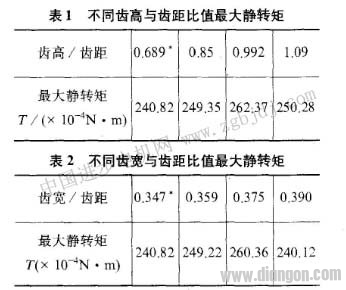
进电动机不同的定转子齿形配合作过一些基础研究，以探明它们对电机性能的影响，所得出的结论是，定转子的齿形应选用矩形为好。但是，在齿形尺寸上，例如齿高、齿距和齿宽彼此之间是否存在一个最佳的配合，为此，我们对该样机采用不同的齿高与齿距的比值（在同一槽宽时）以及不同的齿宽与齿距的比值（在同一槽高时），进行最大静转矩的计算，表l和表2分别列出它们的计算结果（均为两相同时通电状况），其中表示样机的实际尺寸。由表可见，磁阻式步进电动机定转子齿形除了采用矩形之外，其齿高应尽量接近齿距，齿宽则约为齿距百分之的37.5。

a．为充分考虑电机的饱和因素，本文从整个电机磁场的磁共能出发，计算了反应式步进电动机单相通电和两相同时通电的静态转矩特性，且计算值与实测值基本接近，说明此理论计算方法是正确的。

b．当齿高／齿距≈_l和齿宽／齿距≈0.375时，磁阻式步进电动机可获得较大的静态转距，这在工厂的生产中可作参考。