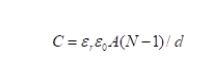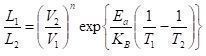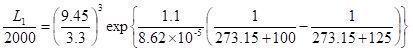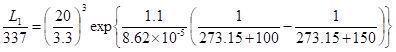一种陶瓷贴片电容失效率以及寿命的评估方法
|
1. 陶瓷电容发展现状与趋势 陶瓷电容自诞生以来,就朝着小尺寸、大容量的趋势发展。近年来,0201和0402封装已成为行业主流,这两种封装的需求量已超过总需求的70%;01005、008004等更小封装产品也相继面世,且需求量逐年增加。在容值方面,100μF、220μF、330μF等大容量产品已在行业内大量使用,日本太阳诱电在19年宣布了可量产1000μF陶瓷电容。陶瓷电容器容值的计算公式如下。式中,C为电容量,εr和ε0分别表示陶瓷介质介电常数和真空介电常数,A表示内电极有效面积,d表示陶瓷介质厚度,N表示内有效内电极层数。
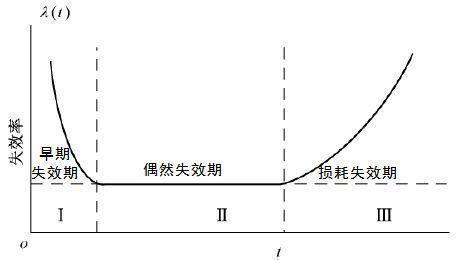
(1) 由公式1可知,为实现小封装和大容量特点,就必须在相同尺寸的电容内堆叠尽可能多的层数(增大N值),且需要降低介质层的厚度(减小d值),目前日系厂家介质厚度已经能实现0.3μm以下。层数的增加以及介质层厚度的减小,都对陶瓷电容原材料和制造工艺提出了巨大的挑战,生产过程中细小的异物或空洞都将造成致命的影响。同样,由于小封装和大容量的发展,陶瓷电容设计的余量越来越小,对用户提出的要求越来越高,在选型时对陶瓷电容失效率和极限寿命的评估也显得十分必要。 2. 浴盆曲线 实践证明大多数设备的故障率是时间的函数,典型故障曲线由于形状呈现出两头高,中间低,所以被称为“浴盆曲线”。浴盆曲线同样适用于表示陶瓷电容的故障率。浴盆曲线中第一阶段为早期失效,如前所述,陶瓷电容早期失效多数在厂家生产过程中的电性能加严筛选阶段被剔除,或发生在客户焊接电容过程中,如生产撞件和单板弯曲应力;第二阶段为偶然失效期,此阶段失效率较低且处于平稳期,此阶段失效常见的原因为零星的电容内部存在无法剔除的细微缺陷,在损耗失效期前提前暴露;第三阶段为损耗失效期,主要由于电容的老化造成,即接近到达了电容的寿命终点,此阶段随着时间的变化故障率呈现出迅速上升趋势[1,2]。对于陶瓷电容,第一阶段失效能够被有效剔除和及时发现,所以重点关注的是第二阶段的失效率,以及进入第三阶段的时间,即极限寿命。
图1 浴盆曲线 3. 陶瓷电容加速寿命换算与失效率计算公式 陶瓷电容一般通过加速试验的方法对寿命进行换算。常见的计算公式是基于Arrhenius加速模型得到,Mogilevsky和Shirn在陶瓷电容加速寿命试验文章中提出的公式为[3,4]:
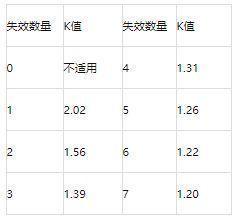
式中,L1为需要换算条件下的寿命,L2为实际加速试验结果的寿命;V1和V2分别为需换算条件下的电压和实际加速试验条件的电压;T1和T2分别为需换算条件下的温度和实际加速试验条件的温度(开尔文温度);n为电压加速因子,通常取3~5;Ea为活化能,通常取1.1~1.3eV;KB为玻尔兹曼常数(8.62×10-5eV/K)。失效率可用Fit来进行表示,计算公式如下: FR=(r/T)×K×109 (Fit) (3) 公式中,r表示试验过程中电容的失效数量(如果无失效,则式中r×K=0.917);T表示试验样品数量与试验时间(或换算时间)的乘积;K为60%置信度下的常数,具体取值见下表1。 表1 不同失效数量对应K值
4. 偶发失效期失效率评估方法 为评估陶瓷电容在正常服役条件下偶发失效期的失效率,一般采用大样品量(1000~10000颗)、低加速应力(1~1.5倍额定电压)、长时间(1000~2000h)的试验方案,根据试验结果计算评估实际使用条件下的Fit值。 4.1 试验方法与结果 选取市场上某品牌温度特性:X7S,电压:6.3V,容值:47μF±20%,封装:1216(X7S-6.3V-47μF±20%-1210)的陶瓷电容,数量1000颗,将电容焊接在测试板上,在上限工作温度125℃、1.5倍额定电压9.45V条件下试验2000h。实时监控电容的IR值,当IR下降至一定程度后判定为失效。在此条件下此次试验完成2000h试验后该规格电容失效数量为2颗。 4.2 失效率计算 假设此规格电容在用户处正常工作条件为100℃、3.3V,要计算此条件下偶然失效期的失效率,首先通过公式2将试验条件125℃、9.45V的2000h换算得到100℃、3.3V条件下的时间(取电压加速因子为3,Ea为1.1):
计算结果L1=402000h,即电容在125℃、9.45V试验2000h,相当于在100℃、3.3V下工作约402000h。得到此时间后,再根据公式3来计算电容在100℃、3.3V条件下的偶发失效率: FR=(2/1000*402000)×1.56×109 (Fit)=7Fit 综合以上计算,可得到这个规格电容在100℃、3.3V下工作,偶然失效期的失效率约为7Fit。当然,根据实际情况,如果电容在不同的条件下工作,通过以上公式也能得到不同实际使用条件下的失效率。值得注意的是,此试验中失效电容是处于偶然失效期,因此得到的试验结果只能用来评估失效率,而不能用于来衡量损耗失效期的寿命。另外,失效率计算结果可能会随着试验样本量、试验时间以及试验条件变化而变化,试验样本量越大、试验时间越长、试验条件越接近于实际使用条件,得到的结果越真实,但是受到试验设备和时间的限制,不能无限的增大数量和延长时间,所以可以根据实际情况调整样本量和试验条件。 5. 损耗失效期寿命评估方法 仅仅评估电容在偶然失效期的失效率还是不够的,失效率虽低但如果在短短两三年时间内就进入了磨损失效那同样也是不能满足要求的。因此,用户还希望知道电容的使用寿命,知道电容在什么时候会进入到损耗失效期。为评估电容的损耗期寿命,一般通过高加速应力试验(150℃或以上高温,3~5倍额定电压),使电容进入到损耗失效阶段发生大量失效,再根据试验结果结合韦伯分布拟合,评估电容在实际使用条件下的寿命。 5.1 试验方法 取某品牌规格为X7S-6.3V-47μF±20%-1210的陶瓷电容,数量20颗,焊接在测试板上,在150℃、20V电压下进行试验,实时监控每一颗电容的漏电流值,当在高温下漏电流超过一定值后判定为失效,试验持续进行直至20颗电容完全失效。
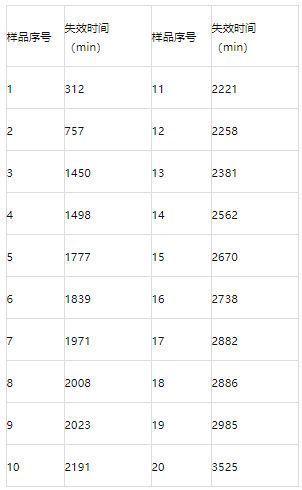
图2 测试电容焊接在测试板上 5.2 试验结果与寿命评估 记录此规格在150℃、20V下20颗样品失效时间如下表2。
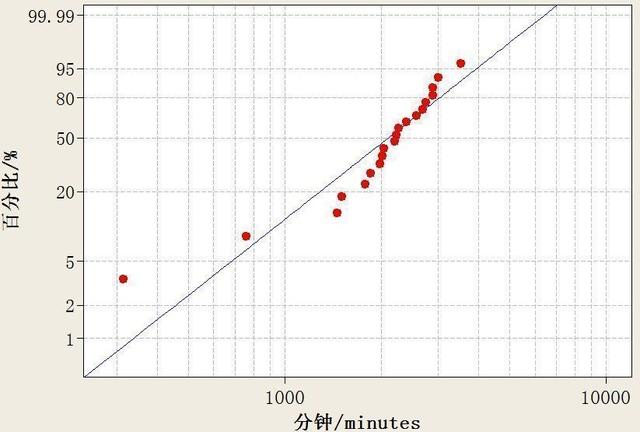
表2 试验样品失效时间 韦伯分布是瑞典物理学家Weibull教授提出的一个数学模型,是近年来在寿命可靠性分析中使用最广泛的模型之一。根据测试结果,通过韦伯分布拟合得到如下图3曲线。
图3 试验结果韦伯拟合曲线 在此类试验中,通常情况下陶瓷电容行业内日系品牌取B1时间(1%失效率时间)来换算实际使用条件下寿命,此试验结果通过韦伯分布拟合得到B1为337min。同样,假设此规格电容在用户处正常工作条件为100℃、3.3V,那么通过公式2和B1可得到在此条件下此电容的寿命约8.12年(取电压加速因子为3,Ea为1.1)。同样,如果电容在其他条件下工作,也可以通过同样的方法计算不同条件下对应的寿命。
综合以上结果,该规格为X7S-6.3V-47μF±20%-1210的电容,如在100℃、3.3V下工作,运用以上两种方法,通过计算得到偶然失效期失效率约为7Fit,工作大约8.12年后会进入到磨损失效期。通过以上实验,不仅能评估电容在服役期间的偶发失效率,还能够评估电容的进入损耗失效期的时间。更重要的是,通过试验可以为用户提供选型指导,如此使用条件下(100℃、3.3V)计算得到的失效率或寿命不能满足产品需求,用户可以进行更大程度的降额,从而降低失效率和延长寿命。 6. 结束语 本文结合浴盆曲线,分别介绍了陶瓷电容在偶然失效期的失效率,以及在损耗失效期的寿命计算方法,并提出运用两种方法同步进行评估,综合两个试验结果对选型进行指导。运用此方法能够对陶瓷电容的整体性能有全面的把控,用户也可以根据试验结果调整降额条件,使电容在适当的环境下长期稳定的工作,避免电容在服役过程中发生高比率失效或过早进入损耗期。 |