电机的振动、结构噪声和空气噪声产生的基础原理（一）

噪声和振动都是振荡，即周期性地发生的状态或条件的变化，它们描述一个振荡的周期或频率的持续时间和其状态随时间（振幅）的最大值。一些运动可以通过周期性变化的力产生，例如曲柄机构中遇到的力（强迫激励），一些可以通过各种能量储存之间的自发能量交换而独立产生，例如弹性（储存变形能量）和惯性质量（储存动能）之间的能量交换，如果这些储存能够以某种方式被激发（例如：秋千、铃铛、小提琴弦、口哨），由这些能量储存控制的振荡称为自然振荡。

它的频率（固有频率）通常由能量储存的特性决定，而不是由储存在其中的能量决定，由于不可避免的阻尼会导致能量“损失”（例如：材料改变形状时所消耗的能量）。除非将适当的能量源进一步应用于系统，否则自然振荡不能无限期地保持下去。由于振荡系统的特性，通过适当的强迫激励提供能量外，随着时间的推移而保持恒定的能量供应可以产生自我控制的，即自我产生的自然振荡（例如摩擦引起的振动、口哨声）。

除了随着时间的推移表现出来外，自然振荡也总是有其峰谷（自然波形）的特定空间分布，没有破坏力通过安装系统作用于振荡系统时，才能形成自然振荡。自然波形在整个波形中可以同时具有相同的运动偏移，当发生这种情况时，其弹性变形模式r＝0。例如，当一个环发生振荡时，它会随着时间的推移在所有方向上以相同的方式改变其直径时。

如果自然波形的特征在于同时具有两个最大值但相反的振荡偏移振幅（振荡波峰）和两个点之间，在它们之间没有运动（振荡节点），则其具有r＝1的模式。电机的弯曲振动说明了安装系统如何阻碍波形的形成，如果不在轴承处阻止径向振动，则径向振动会受到阻碍。在这种情况下，在转子的圆周上的两个相对点处，径向运动是最大的，但在90°偏移的点处等于零，从圆周方向看，模式为r=1。但在轴向方向上，在轴承之间只能看到一个单一的波腹，在轴承之间只能看到一个单一的波腹，轴承阻碍弹性变形模态r=1的自由形成，因此，轴承中产生径向交变力（振动力）。

如果转子不受轴承的阻碍，它将在两端向与转子中间振动相反的方向振动，并在两端之间形成两个节点。如果将轴承放置在节点处，并允许轴的外端自由振动，则不会阻碍自由转子弯曲振动。当存在阻碍轴承时，就建立了弹性变形模式r=1，轴承系统及其弹性和质量作为振动系统的一部分，相应的弯曲固有频率不同于无轴承转子的弯曲固有频率。

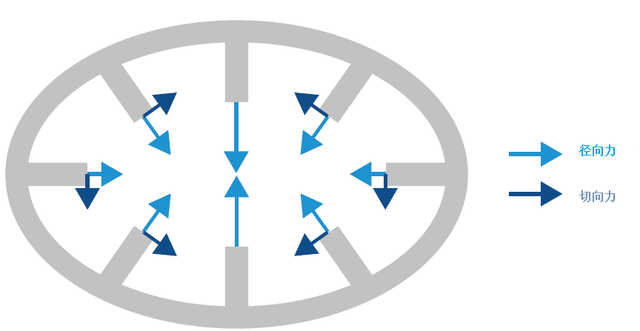
管状金属封装的椭圆变形特征为弹性模式r=2（沿圆周方向的两个全波、四个波峰、四个节点等）。波腹和节点可以改变相对于时间的位置，则模式保持不变。具有两种以上储存各种形式能量（如势能和动能）的结构能够对应的各种固有频率和波形的多种不同的自然振荡，即在时间和空间上相互叠加的若干不同的波腹和节点。