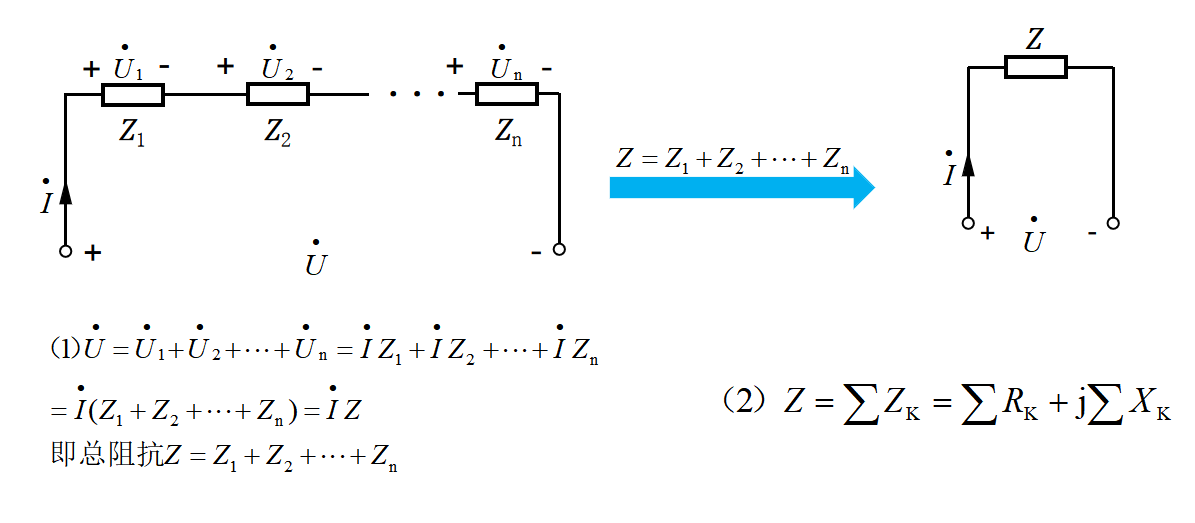电气新手必知：电阻电感电容串联交流电路（专业电气学姐带你学三十三）

  在上一次的学习中，我们知道了电阻元件(本文的电阻元件均指线性电阻元件)、电感元件(本文的电感元件均指线性电感元件)与电容元件(本文的电容元件均指线性电容元件)在直流电路和交流电路中的区别，还知道了三种元件的单一参数交流电路特性。

举一反三，如果交流电路中同时含有电阻、电感和电容或含有其中两种参数，那么该交流电路的特性又是怎样的呢?这就是我们这次的学习内容：“电阻电感电容串联交流电路”，也就是我们(píng)时所说的“RLC串联交流电路”。

  下图33-1的(1)所示为简单RLC串联交流电路。若给该电路通以直流电，由于电容元件的隔断直流的作用，该电路中是没有电流流过的。但给它通以正弦交流电时，根据我们上次所学的内容，该电路除了会有电阻外，还会有感抗和容抗的存在。这里的电阻、电感和电容之间的关系又是怎样的呢?

图33-1

首先，在同一交流电路中，各电气量的角频率ω(频率f)都是相同的，这在之前我们学习正弦量的时候已经提过。回顾上一次的学习内容，在R、L、C的各个单一参数交流电路中，流过电阻元件的电流与电阻元件两端的电压同相;流过电感元件的电流滞后于电感元件两端的电压90°;流过电容元件的电流超前于电容元件两端的电压90°，感抗XL=ωL，即U =IXL，且容抗XC=1/ωC，即U =IXC，结合已知条件：电流的瞬时值表达式和相量式，我们就可以推理出RLC串联交流电路的电压和电流关系。

  如上图33-1的(2)瞬时值表达式和(3)相量式。在图33-1的(2)式中，计算变换过程大家看看即可，由电压u的瞬时值表达式中，我们可以看到，RLC串联交流电路的电压等于各个元件两端电压瞬时值的代数之和，而不是有效值的简单相加，还要考虑相位关系。

同理，图33-1的(3)相量式更为直观，从电压的相量式中，我们可以看到，其虚部(即乘以90°旋转因子部分)是感抗和容抗的差，这是因为感抗和容抗两者上的电压方向相反，一个滞后电流90°，一个超前电流90°，相互抵消。

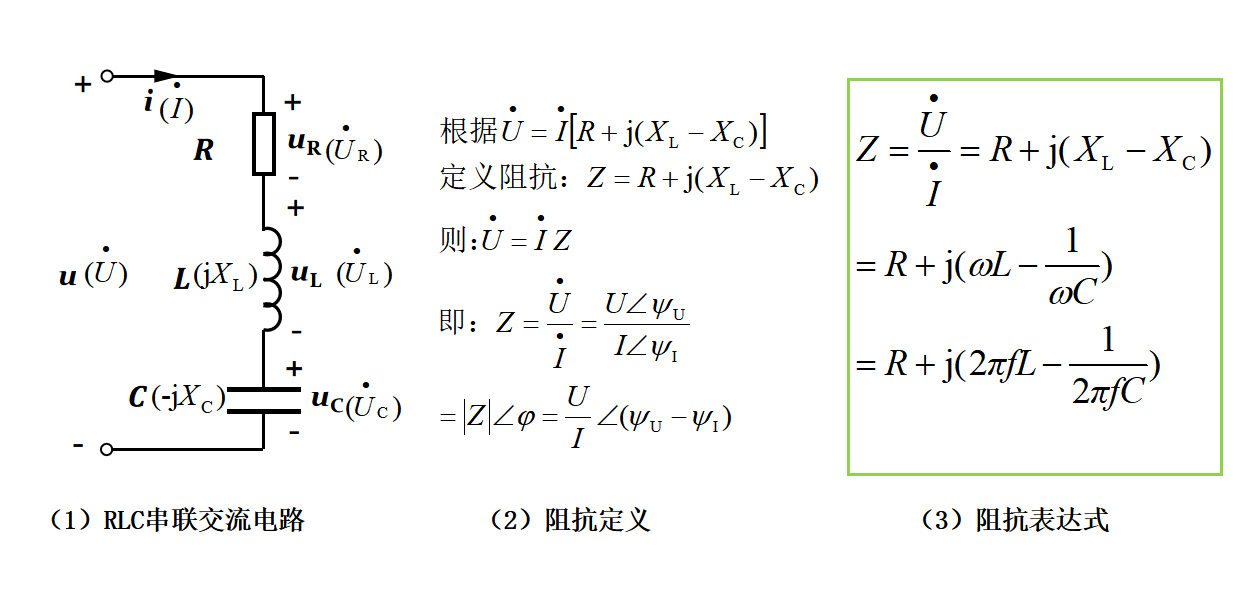
根据图33-1(3)的电压相量式，即电压相量等于电流相量乘以某定值(频率不变)的这种表达式，定义阻抗Z(又称复阻抗)，如下图33-2所示，它是由电路参数决定。

图33-2

  图33-2(2)所示的阻抗，定义为电压与电流的比值，常用Z表示，单位是欧姆(Ω)。阻抗也是一个复数，其实部称为电阻R，虚部称为电抗X，这在上一次的学习中也有所提及。这里要提醒的一点是，阻抗不是相量，这是因为相量是正弦量的表示形式，而阻抗不是正弦量，所以阻抗符号Z上面不能像电压相量、电流相量那样在上面加点。

  根据阻抗的定义，从电压相量除以电流相量的值中，可以发现，阻抗的模(大小)为电压有效值U与电流有效值I的比值，而辐角为电压u与电流i的相位差。根据感抗与容抗的定义、角频率与频率的关系，可得阻抗的集中表达式，如图33-2(3)所示，这几种表达式在电路分析中都比较常用，所有大家很有必要熟记。

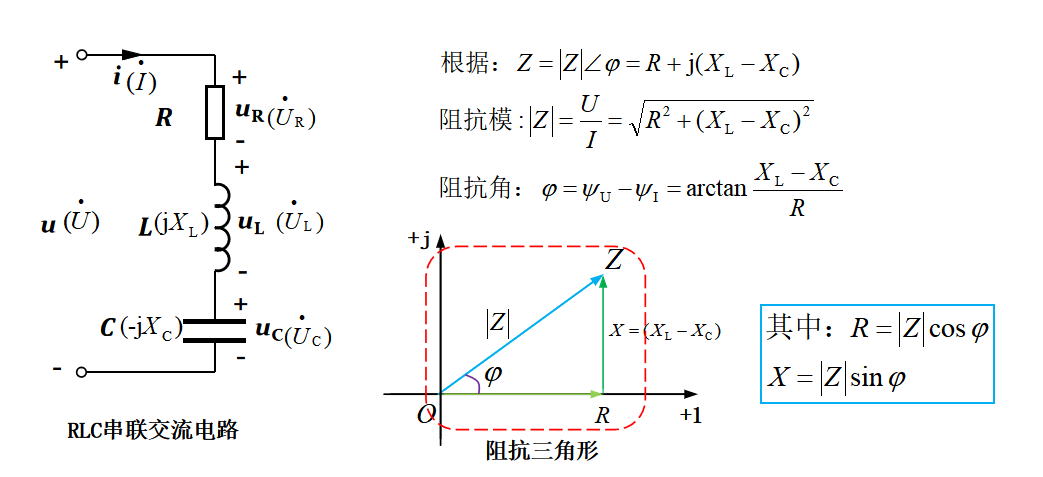
图33-3

阻抗由电阻和感抗、容抗组成，当电路中没有电感元件时，显然，电路中也就不会有感抗，即此时阻抗中只有电阻和容抗;同理，当电路中没有电容元件时，显然，电路中也就不会有容抗，即此时阻抗中只有电阻和感抗。

另外，阻抗既然是一个复数，那么它显然可以在复(píng)面上表示，如图33-3所示。根据阻抗在复(píng)面上的表示，可以看到，其电阻、电抗与阻抗组成一个三角形，这就是大家(píng)常所说的阻抗三角形，图示的阻抗三角形中感抗大于容抗，即X=XL-XC>0，此时的辐角大于零。阻抗模就是上文所说的电压有效值U与电流有效值I的比值，阻抗角为电压u与电流i的相位差。

显然，阻抗、电阻、电抗和阻抗角之间可以用三角函数进行转化和计算，例如阻抗角可以用电阻和电抗的反正切函数关系求得，已知阻抗值的情况下用余弦函数和正弦函数求得电阻和电抗，如图33-3所示。

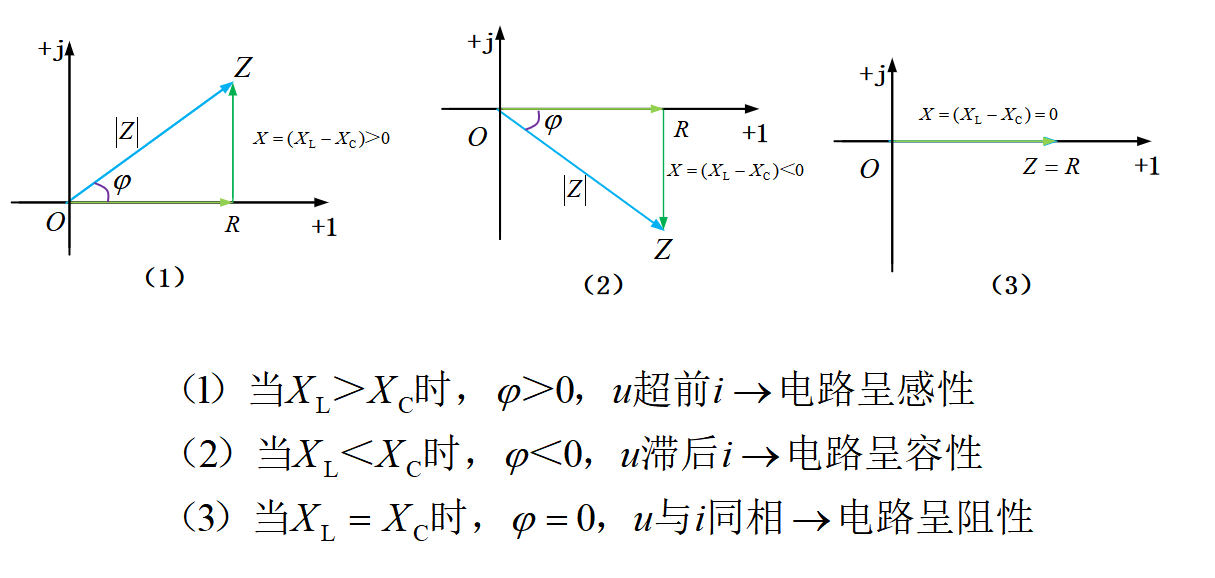
电抗为感抗与容抗的差，即X=XL-XC，结合阻抗三角形，可以得到以下电路参数与电路性质的关系如图33-4所示。

图33-4

  根据图33-4中内容，当感抗与容抗的差不同时，电路会呈现不同的性质，相角也会随之变化。当感抗大于容抗时，电路呈感性，此时阻抗角大于零，即电路中电压超前电流;当容抗大于感抗时，电路呈容性，此时阻抗角小于零，即电路中电压滞后电流;而当感抗等于容抗时，两者大小相等方向相反，电抗为零，此时电路呈阻性，电压与电流同相。

  实际工作中的电容补偿，其依据其实就是电路中感抗和容抗的不同关系，例如在感性负载(如交流电动机)的交流电路中，此时电压超前电流，为了减小电压与电流之间的相角(即功率因数角)，可以在电路中适当接入电容器，以抵消电路中的部分感抗，使得阻抗角变小，提高有功功率。

当补偿后电路依然呈感性，这种补偿方式称为欠补偿;当完全补偿时，即补偿后电路依然呈阻性，这种补偿方式称为全补偿;当补偿后电路依然呈容性，这种补偿方式称为过补偿。

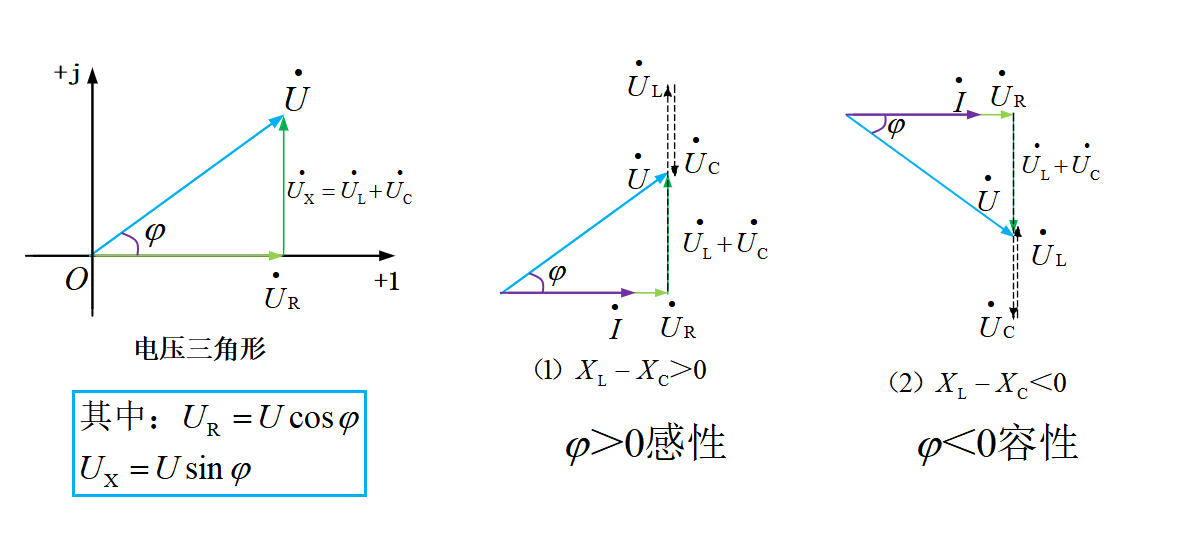
  在RLC串联交流电路中，当以电流相量为参考相量时，各元件的电压是由该元件的参数(电阻、电感、电容)所决定的，包括其数值和相角。所以，结合阻抗三角形和电压电流关系，可以画出电压三角形如下图33-5所示。

图33-5

  根据图33-5所示可以发现，电压三角形的相角其实和阻抗角相等，这是因为在交流电路中，根据图33-2中阻抗的定义，电流相角已知的情况下，电压相角就是由电路参数(即电阻、电感和电容)所决定。

  结合我们之前所学的相量运算，当感抗大于容抗时，如图33-5(2)所示，电阻电压相量、电感电压相量与电容电压相量相加，各元件电压相量首尾相连，此时电压与电流的相角大于零，电路呈感性，同理可以得到电路呈容性时的电压三角形如图33-5(3)所示。

  在上一次学习了单一参数交流电路时，我们知道了电阻元件在交流电路中总是消耗电能的，而电感元件和电容元件是储能元件，它们不消耗电能，只是和电源进行能量的交换。举一反三，在RLC串联交流电路中，因为同时存在电阻、电感和电容，所以电路在是在消耗电能的同时，还进行着能量的交换。此时，该RLC串联交流电路的功率关系如下图33-6所示。

图33-6

  图33-6的各个功率计算过程大家可以不管，只需记得终结果即可。在图33-6(1)所示的瞬时功率表达式中，其两个相加项有着不同的含义，左边部分的值总是大于零，代表了耗能元件上的瞬时功率;

  而右边部分有大于零和小于零两种情况，代表了储能元件上的瞬时功率。也就是说，在每一瞬间，电源提供的功率一部分被耗能元件消耗掉，一部分与储能元件进行能量交换。

  根据图33-6(2)所示的(píng)均功率表达式，(píng)均功率(又称有功功率)P为电压与电流乘积的余弦值，其中cosφ称为功率因数，它是用来衡量负载对电源的利用程度。结合上次所学的无功功率知识，得RLC串联交流电路无功功率为图33-6(3)所示，其中(XL-XC)表明电感和电容与电源之间的能量互换。

图33-7

  根据电压三角形，把电阻电压有效值乘以电流有效值即为有功功率的值，它是总电压与总电流有效值乘积的余弦值;

  同理，把电抗电压有效值乘以电流有效值即为无功功率的值，它是总电压与总电流有效值乘积的正弦值。根据有功功率和无功功率的这种三角函数关系，定义视在功率S如下图33-8所示，它是电路中总电压与总电流有效值的乘积，用符号S表示，单位是伏安(VA)。

图33-8

  和阻抗三角形一样，有功功率、无功功率与视在功率在复(píng)面上也可以组成功率三角形。显然，视在功率也不能用相量表示，因为它不是正弦量。比较阻抗三角形、电压三角形和功率三角形，可以发现，它们之间是由关联的，即将电压三角形的有效值同除电流有效值，就可以得到阻抗三角形;将电压三角形的有效值同乘电流有效值，就可以得到功率三角形。

  在电路中，电阻、电感和电容都可以进行串并联，而由电阻、电感和电容组成的阻抗显然也可以进行串并联。我们这次就先学习阻抗的串联，下次再学习阻抗的并联。

图33-9

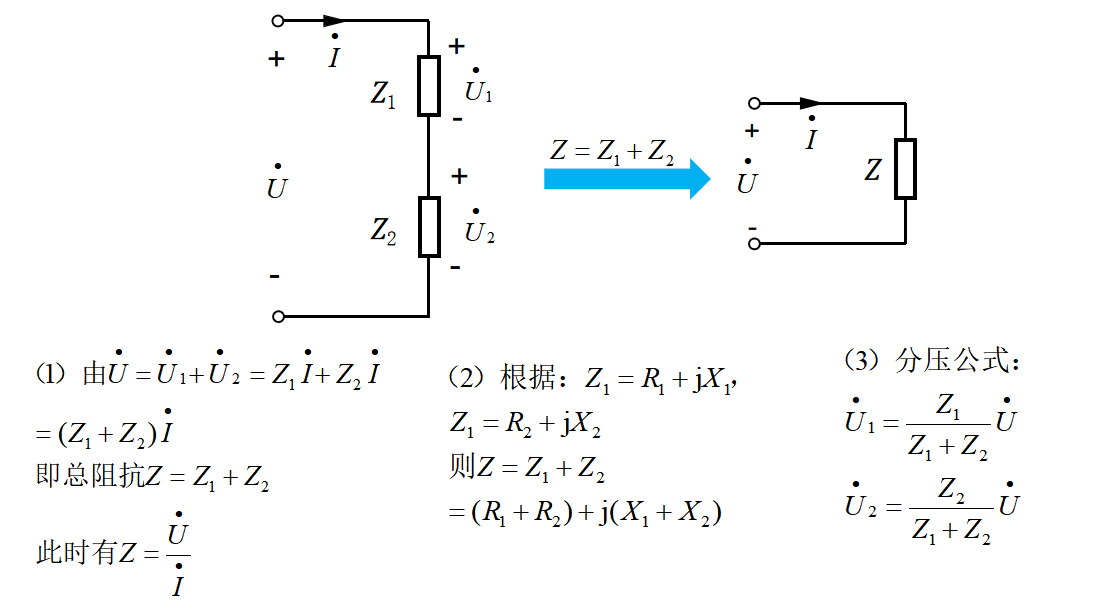
  电阻的串联是将各电阻直接相加得到等效总电阻，流过各个电阻的电流一样，各个电阻上的电压之和为总电压......阻抗的串联其实和电阻的串联很相似，也是将各个串联阻抗相加得到等效总阻抗，如图33-9(1)所示。

  不同的是，阻抗的相加并不是简单的数值相加，而是复数的运算，如图33-9(2)所示，;两个阻抗相加，分别将其实部与实部相加得到电阻部分的值，虚部与虚部相加得到电抗部分的值。

  阻抗串联交流电路中，各个阻抗对总电压也有分压作用，但是此时的分压是相量的运算，如图33-9(3)所示。

图33-10

  将图33-9(1)式进行推广，得到多阻抗串联电路的一般式，如上图33-10所示。显然，多阻抗串联电路的等效变换理解起来并不难，但是其实际的计算相对麻烦，因为其中涉及到数值与角度相互关联。

  另外，阻抗本身也包含的电阻、电感和电容三个参数在里面。在《电工基础》课程中，曹老师花费了两个多课时的时间讲解习题，旨在让学员们快速理解RLC串联交流电路与阻抗串联交流电路。

  在这里再次强调一下，相量的运用，包括对它的理解与运算，在电路分析中是非常实用的，希望大家能掌握这部分的内容。在一开始所学的直流电路比交流电路简单很多，而交流电路和直流电路又有很多相似的地方，所以先易后难、先直流后交流是学好《电工基础》的佳方法。

  后，RLC串联交流电路的学习已经完成，希望大家能学以致用，把学到的知识运用到实际工作中。(技成培训原创，作者：杨思慧，未经授权不得转载，违者必究!)

相关课程：

电工基础