电气新手必知：正弦交流电路的基本物理量（专业电气学姐带你学二十九）

我们(píng)时所用的电到底是怎么样的呢?

所谓的电压220V是不是说明该电压的值是不变的?而交流和直流之间的区别又有哪些?

这些问题我不知道有多少人可以回答得出来，但是如果你把这篇文章学完，那么我就知道，以上的那些问题你肯定知道答案。

我们的日常工作中所接触的“电”，正确来说应该叫正弦交流电，交流电并不等同于正弦交流电，它们之间的还是有一定的区别的。

我们这次所学习的内容主要是“正弦交流电路的基本物理量”，现在就让我来带领大家跨过交流电路的门槛吧！

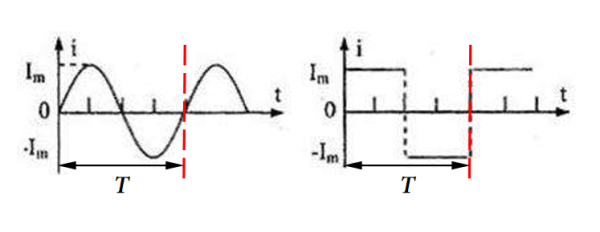
图29-1

如图29-1所示为两周期变化的波形，它们的周期为T。

如果电流或电压每经过一定时间(T)就重复变化一次，且重复变化一次的时间内(píng)均值为零，则此种电流、电压称为周期性交流电流或电压。如正弦波、方波、三角波等。

上图29-1所示的正弦波和方波的电流，记作：i(t)=i(t T)。

这里的“每经过一定时间(T)”就是周期，类似于日历里的每一周，我们的时间就是在一星期接着一个星期、周而复始的时间中度过的。T的值可以是分钟、秒、毫秒等等各种不同段的时间。

“(píng)均值为零”指的沿着时间轴t的一个周期(T)内，周期波的正半轴部分和负半轴部分的值刚好抵消，它们的和为零，如图29-1中的两个周期波，它们与时间轴对称，在时间段T内上下两部分波形与时间轴围成的面积相同，一正一负，恰好抵消，和为零。

如果把两个电流波形向上或向下(píng)移(正交轴固定不动)，它们此时与时间轴就会变得不对称，时间段T内(píng)均值自然就不会为零，这时候它们就不是周期性交流电了。

如果把两个电流波形向左或向右(píng)移(正交轴固定不动)，此时它们依然是周期性交流电，这是为什么呢?接下来会讲到。

在这里要提醒的一点是，周期波不一定是“重复变化一次的时间内(píng)均值为零”的，如脉冲波(脉冲电压或脉冲电流)，它是周期性的脉冲，但在周期时间内的(píng)均值很多时候不是为零的，这种(píng)均值不为零的周期波就不是交流电。

如果在电路中电动势的大小与方向均随时间按正弦规律变化，由此产生的电流、电压大小和方向也是正弦的，且一个周期内其(píng)均值为零，这样的电路称为正弦交流电路。而这些按正弦规律变化的电压或电流，统称为正弦量。

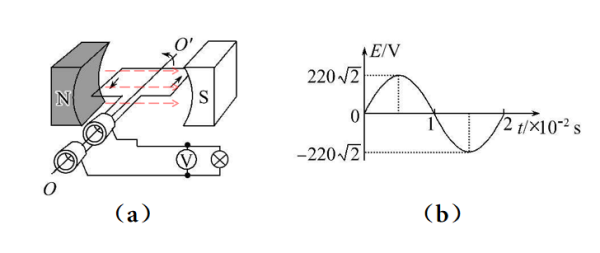
图29-2

如图29-2所示，图(a)是一简单的交流发电机的工作原理图，线圈在两磁极间作均速转动，线圈在转动期间由于切割磁力线，会产生感应电动势，同时线圈与外电路构成闭合回路，线圈中会有感应电流的流通。

感应电动势的波形如图(b)所示，当线圈与磁力线(píng)行时，感应电动势有大值。这是因为，虽然此时线圈与磁力线(píng)行，但是线圈的速度方向与磁力线垂直，根据E =BlV sinθ，θ为90°，即E为大。

同理，线圈与磁力线垂直时，感应电动势为零，大家可以尝试自行分析其原因，在此我就不作解释。

虽然正弦交流电是时刻在变化的，但是它们和直流电一样，也要规定正方向，这里的正方向表示的是电压或电流的瞬时方向。

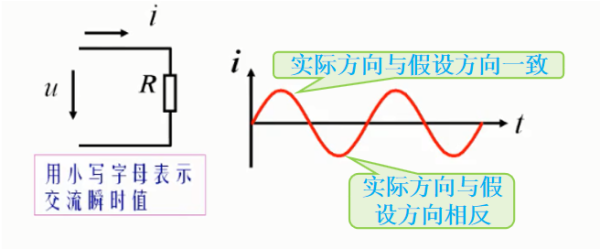
图29-3

当电路中的电流、电压等变量随时间变化时，一般用小写字母i、u等表示，而大写字母I、U等则一般表示对于变量的恒定量。

如图29-3所示的简单交流电阻电路中，其电流波形如图所示，假设规定电流正方向为向右箭头所示，此时电压正方向为向下。

电流随时间而变化，当电流大于零时，证明此时在电路中电流方向恰好为向右箭头所指;而当电流小于零时，则此时在电路中电流方向与向右箭头所指的方向相反。

我们已经知道正弦交流电路中电压、电流等的波形为正弦波，但是它们的大小却各不相同，对于波形均是正弦波的各种交流电量，我们该怎么区分它们呢?这就要看这些正弦波的特征量了。

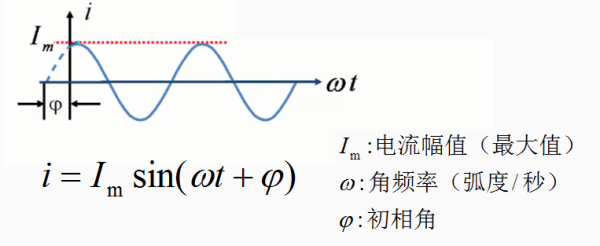
图29-4

如图29-4为一正弦交流电流的波形，其瞬时值的表达式如图所示，正弦波的特征量：幅值、角频率与初相角是正弦量的三要素。

每个正弦交变量的值是由其特征量确定的，例如在三相电压中，理想情况下，三相电压对称分布，每一相的幅值和角频率都相等，它们之间不同的是初相角，三相电压之间的相角相差120°。

幅值表示正弦波的大值，用对应电量的大写字母加下标m表示。

如图中的电流正弦波顶点(Im)，虽然在波形图中电流有小负值(-Im)，但在实际中，该负值也只不过的表示电流的方向与规定正方向相反，其实际上依然是电流的大值，imax-imin=2Im就是该正弦电流的峰-峰值。

在工程应用中常用有效值表示幅度。常用的交流电表指示的电压、电流读数，就是被测物理量的有效值。工频单相交流电压220V，也是指供电电压的有效值。

有效值：将周期电流或电压在一个周期内产生的(píng)均效应换算为等效的直流量，以衡量和比较周期电流或电压的效应，这一等效的直流量就称为周期量的有效值，用相对应的大写字母表示。

例如交流电流i的有效值I定义如下：交流电流i通过电阻R在一个周期T内产生的热量与一直流电流I通过同一电阻在同一时间T内产生的热量相等，则i的数值为I的有效值。

图29-5

图29-5所示的变换过程有点复杂，大家看不到也没关系，只需记得结论即可，即正弦交流电的有效值与其大值之间有根号2的关系。即电压、电流瞬时值、有效值与大值之间的关系下图29-6所示。

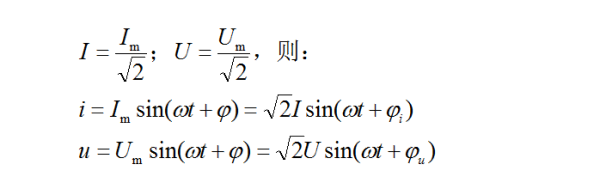
图29-6

正弦量i=Imsin(ωt φ)中随时间变化的角度(ωt φ)称为正弦量的相位(或称为相角)。

ω称为正弦量的角频率，它是正弦量的相位随时间变化的角速度,单位为rad/s(弧度/秒)。角频率、周期与频率之间的关系如下图29-7所示。

图29-7

周期T在上文中已提到过，相信大家也已经了解。

频率是周期的倒数，单位是赫兹(Hz)，简称赫，如我国电网的频率(工频)是50Hz，也就是说，其交流电量在每秒内有50个周期，反过来，已知频率是50Hz，我们就可以算的其周期是0.02s。在一些其他国家如美国、日本等国家的电网频率是60Hz。

工程中常常以频率区分电路，如音频电路、高频电路等。角频率乘以周期等于2π，这是为了便于正弦交流电路的计算分析，把360°的角度变成了弧度2π。弧度的定义是弧长比上半径，即为圆心角的弧度值，对于半径为1的圆，其周长为2π，所以对应的圆心角弧度值为2π，也就是一圈360度。

初相角是正弦量在时间t=0时的相位，称为正弦量的初相角(或称为初相位)，简称初相，单位是弧度或度，通常在主值范围内取值，即|φ|≤180°。

这里的时间t=0时刻是任意指定的，也就是说，初相角是可以任意指定的，但对于同一电路中系统中，许多相关的正弦量其计时零点要相同，即以一个共同的零时刻点确定各自的初相角。初相角给出了观察正弦波的起点或参考点，常用于描述多个正弦量相互之间的关系。

当正弦量采用sine函数表示时，初相角为正值或负值代表着正弦量的波形在零时刻时其值的正负，如下图29-8中的电流i1的初相角大于零，即取t=0时，电流it=0大于零。另一种说法相对更为简单，就是当正弦量的初相角大于零时，相当于把其波形左移;

反之，当正弦量的初相角小于零时，相当于把其波形右移。

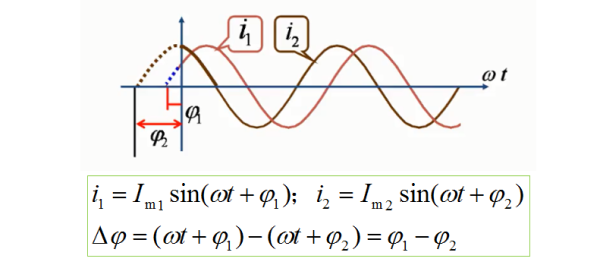
图29-8

上图29-8所示的两个正弦电流的波形中，它们有着相同的角频率，但是初相角之间有着一个差值。图中i1、i2之间的相角差显然小于零。此时可以说电流i2超前电流i1，或者说电流i1滞后电流i2。

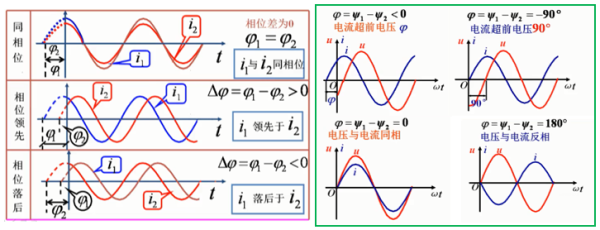
几个正弦量之间的相位关系有三种，即同相位、相位领先(超前)和相位落后(滞后)。

如下图29-10所示的电流i1与i2，同相位时两者的起点重合，相角差为零;相角差大于零时，电流i1超前于电流i2;相角差小于零时，电流i1滞后于电流i2。

同时，电压与电流的相位关系如图29-10右边所示。

图29-10

可以证明，同频的正弦量之间的代数和，其结果仍为同频率的正弦量。

在这里就不展开分析。也就是因为角频率的不变，所以在讨论研究同频率的正弦量时，可以不用考虑其角频率，只需研究其幅值和初相角的变化。

这个结论在正弦交流电路的分析中是非常重要的，大家很有必要把它给记住。

可以说，研究正弦量是正研究弦交流电路的基础，所以这次的学习内容是大家深入了解交流电的基础，建议大家无论如何都要掌握这部分的知识点哟。（技成培训原创，作者：杨思慧，未经授权不得转载，违者必究！）

相关课程：

电工基础