高阶陶瓷电容失效处理方式方法
|
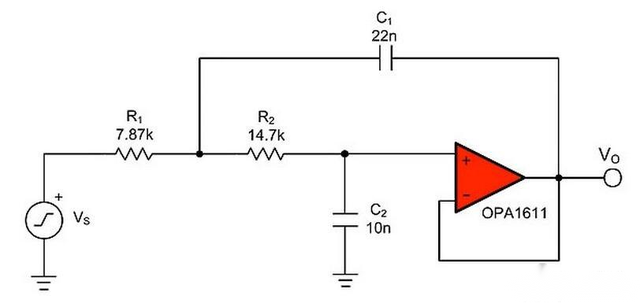
高介电常数mlcc失真示例 在有源滤波器电路、数据转换中使用的去频迭滤波器以及放大器的反馈电容中,采用高介电常数MLCC可能引入电路失真的问题。为了说明这一效应,设计人员使用TI的FilterPro软件设计了一个使用Sallen-Key拓扑的1kHz巴特沃兹有源低通滤波器。有源滤波器是一种常见应用,其中电容失真会降低整个电路的性能。许多设计人员选择降低电容失真对输出噪声的影响而采用较低电阻值,但这样做会增加实现所需拐角频率所需的电容值。因此,在满足电容、电路板面积和成本要求方面,高介电常数MLCC可能成为唯一的选择。 图1展示了滤波器电路,包括无源组件值,使得电容C1和C2可以用不同介电类型、封装尺寸的MLCC进行替代,从而直接比较不同电容类型的性能。在测试中,所有电容都使用了额定电压为50V。
在此示例中,设计人员选择了高性能音频运算放大器(op amp)OPA1611作为低噪声和低失真的基础。为了满足电阻值的要求,设计人员采用了1206封装的薄膜高精度电阻,以最小化除了这些电容之外的失真影响。根据"有源交叉设计",某些电阻类型可能会产生类似于电容的失真[2]。最后,电路使用±18V电源供电,以避免放大器饱和对测量结果产生影响的可能性。 总谐波失真加噪声(THD N)是一个非常有用的指标,可以量化电路中噪声和非线性增加到信号中超出基频的部分。这个值可以表示为谐波和系统RMS噪声电压与基频RMS电压的比值[3]。谐波是输入信号整数倍频率的信号,由于无源组件和集成电路的非线性行为产生。电路的整体噪声可以是集成电路固有噪声、电阻器热噪声,或者是耦合到电路中的外部噪声。方程式1将THD N计算表示为振幅比,其中VF是基频RMS电压,VN是RMS噪声电压,VI是每个谐波的RMS电压。
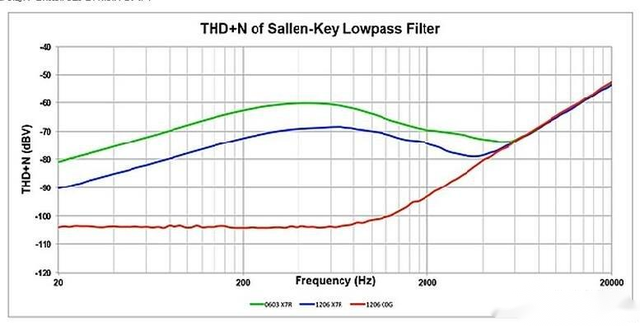
采用500kHz的测量带宽,对20Hz到20kHz频率范围的1Vrms信号进行滤波器电路的THD N测量。图2展示了不同电容类型的电路在1Vrms下的THD N性能(单位为dB)。1206封装的C0G介电类型MLCC表现出卓越的性能:滤波器通频带中的THD N测量值达到了测量系统的噪声底限。我们也对采用0805封装的C0G电容进行了测试,结果表明其具有相同的性能水平,为了简化图表,我们从图中去除了这部分数据。超过滤波器转角频率的THD N增加表明滤波器的衰减能力降低了信号幅度与噪声底限的比值。 如果我们将电容类型更换为采用1206封装的X7R类型,我们会立即观察到电路性能的衰减。在20Hz时,THD N增加最小值为15dB,并在400Hz至800Hz的区域内达到峰值,此时THD N的测量增加了35dB。如果使用更小的0603封装的X7R电容,THD N性能将进一步提高(远超过频谱的10dB)。需要注意的是,在整个测试过程中,我们没有更改滤波器中的运算放大器和电阻器,因此增加的THD N值仅与电路输出信号端的X7R电容产生的额外谐波有关。
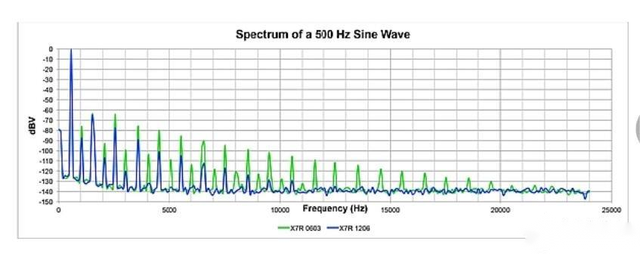
图3显示了在滤波器输出端使用0603和1206封装X7R电容时产生的500Hz正弦波频谱。该频谱显示了大量的基波,主要是奇次谐波。令人惊讶的是,使用0603封装的X7R电容构建电路时,在500Hz输入信号时可以观察到超过20kHz的谐波。
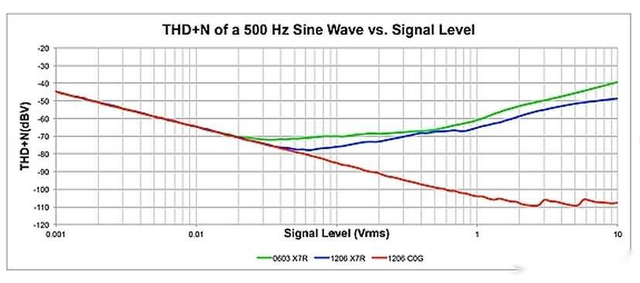
我们的任务是确定高级别的失真源,然而,对于工程师来说,无论是集成电路故障还是无源组件故障,都不是直观可以察觉的。为了确定主要的失真源,一种方法是测量电路在广泛信号电平下的THD N(参见图4)。在图1中,Sallen-Key滤波器的THD N在500Hz基频下显示了1mVrms到10Vrms的信号电平范围。当使用C0G电容构建电路时,随着信号电平的增加,THD N会逐渐下降,最终达到测量系统在2Vrms信号电平下的噪声底限。
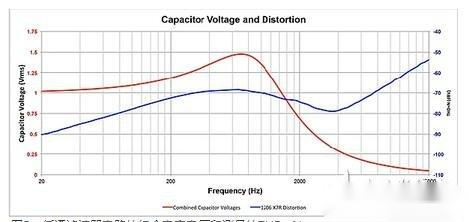
负斜率线表明,由于运算放大器和电阻器的存在,电路噪声是THD N计算的主要影响因素。在这种情况下,随着信号电平的增加,测量的THD N下降,因为信号电压与噪声电压之比增大。相反地,无源组件的非线性在较高信号电平时变得更糟糕,并且随着信号电平增加而引起失真的增加。当滤波电路中的电容被替换为X7R类型时,就会出现这种情况。采用0603封装的X7R电容在20mVrms信号幅度时开始出现失真的上升。采用1206封装的X7R电容呈类似的行为——在40mVrms信号幅度时开始出现失真的上升。因此,如果电路显示出失真随信号电平增加而上升的趋势,无源组件(电阻或电容)最有可能成为限制电路性能的主要因素。 由于无源组件的失真随信号电平的增加而增大,因此滤波器电路在电容施加电压最大时的失真也达到最大。TI的免费SPICE仿真器(Tina-TI)中的AC传输特性分析可用作绘制电路中组件两端电压的频率函数。图5显示了在20Hz到20kHz频率范围内电容C1和C2两端的组合电压以及采用1206封装的X7R电容的滤波器的THD N。个别电容C1和C2的电压是通过均方根值组合的,其在约600Hz处具有最大值。图5清楚地表明电容电压的峰值与失真最大点的高度相关,并且表明电容是导致滤波器输出端失真过大的原因。在两个电容产生不同失真的情况下,两次测量之间可能会存在一些不一致之处。通过确定每个电容的信号增益,我们可以进一步深入分析。
文章内容整理自网络,仅作为学习交流使用,如有侵权请联系沟通 |