开关电源降压-升压电路如何工作

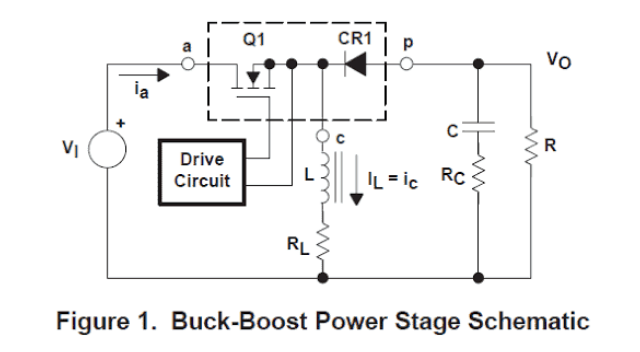
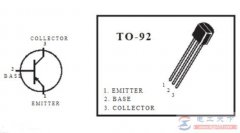
　　我们都听说过很多关于降压和升压电路的知识，并且知道这些电路基本上用于 SMPS 设计，用于在输入端升压或降压给定电压。这项技术的有趣之处在于，它允许上述功能产生可忽略不计的热量，从而实现极其高效的转换。

　　什么是降压-升压，它是如何工作的

　　让我们在不涉及太多技术细节的情况下学习第一部分中的概念，以便即使对于新手来说也更容易理解什么是降压升压概念。

　　在名为降压、升压和降压-升压的三种基本拓扑中，第三种更为流行，因为它允许通过单一配置使用两种功能（降压升压），只需改变输入脉冲即可。

　　在降压-升压拓扑中，我们主要有一个电子开关元件，它可以是晶体管或 mosfet 的形式。该组件通过来自集成振荡器电路的脉动信号进行切换。

　　除上述开关元件外，该电路以电感、二极管和电容为主要成分。

　　在导通状态期间，输入电流通过 MOSFET 获得一条畅通的路径，并立即尝试通过电感器，因为二极管处于反向偏置状态。

　　电感器由于其固有特性试图限制电流的突然施加，并在补偿响应中在其中存储一定量的电流。

　　现在，只要将 MOSFET 关断，它就会进入关断状态，从而阻止输入电流的任何通过。

　　再次，电感器无法应对电流从给定幅度到零的这种突然变化，并且为了对此进行补偿，它通过电路输出端的二极管反冲其存储的电流。

　　在此过程中，电流也存储在电容器中。

　　在 MOSFET 的下一个导通状态期间，循环如上所述重复，但是在电感器没有可用电流的情况下，电容器将存储的能量释放到输出中，这有助于将输出保持在优化的程度。

　　您可能想知道是什么因素决定了输出的 BUCK 或 BOOST 结果？这很简单，这取决于允许mosfet保持在ON状态或OFF状态多长时间。

　　随着MOSFET导通时间的增加，电路开始转变为升压转换器，而MOSFET关断时间超过其导通时间会导致电路表现得像降压转换器。

　　因此，可以通过优化的 PWM 电路对 mosfet 进行输入，以在同一电路上获得所需的转换。

　　从技术上探索 SMPS 电路中的降压/升压拓扑：

　　如上节所述，开关模式电源常用的三种基本拓扑是降压、升压和降压升压。

　　这些基本上是非隔离的，其中输入功率级与输出功率部分共享一个公共基础。当然，我们也可以找到孤立的版本，尽管非常罕见。

　　上述三种拓扑结构可以根据其独有的特性进行唯一区分。这些特性可以识别为稳态电压转换比、输入和输出电流的性质以及输出电压纹波的特性。

　　此外，占空比对输出电压执行的频率响应可被视为重要属性之一。

　　在上述三种拓扑结构中，降压-升压拓扑是最优选的一种，因为它允许输出工作电压低于输入电压（降压模式），也可以产生高于输入电压的电压（升压模式）。

　　然而，输出电压始终可以通过与输入相反的极性获得，这不会产生任何问题。

　　由于相关电源开关 (Q1) 的切换，施加到降压升压转换器的输入电流是脉动电流的形式。

　　这里电流在每个脉冲周期内从零切换到 l。对于输出也是如此，我们得到一个脉动电流，因为相关的二极管仅在一个方向上导电，导致开关周期内的 ON 和 OFF 脉动情况.

　　当二极管在开关周期中处于关断或反向偏置状态时，电容器负责提供补偿电流。

　　本文解释了降压-升压转换器在连续模式和非连续模式操作中的稳态功能，并提供了示例波形。

　　在介绍了 PWM 开关设计之后介绍了占空比到输出电压交换功能。

　　图 1 是添加了驱动电路块的降压-升压功率级的简化示意图。电源开关 Q1 是一个 n 沟道 MOSFET。输出二极管为CR1。

　　电感器 L 和电容器 C 构成有效的输出滤波。本文对电容 ESR RC（等效串联电阻）和电感直流电阻 RL 进行了分析。电阻器 R 对应于功率级输出所指示的负载。

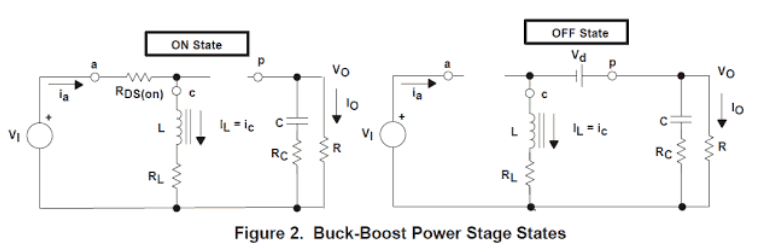
　　在降压-升压功率级的正常功能过程中，Q1 不断地开启和关闭，开启和关闭时间由控制电路控制。

　　这种开关行为会在 Q1、CR1 和 L 的结点产生一串脉冲。

　　即使电感器 L 与输出电容器 C 相连，如果只有 CR1 导通，就可以建立一个成功的 L/C 输出滤波器。它清除连续的脉冲以产生直流输出电压。

　　降压-升压级稳态分析

　　功率级可以在连续或不连续的电感器电流设置中起作用。连续电感电流模式是通过在稳态过程中在开关序列上电感中的连续电流来识别的。

　　不连续电感电流模式由电感电流在开关周期的一部分内保持为零来识别。它从零开始，延伸到最大值，并在每个切换模式的过程中回到零。

　　之后更详细地提到了这两种不同的方法，并提出了电感值的模型建议，以维持选定的功能模式，因为额定负载的能力。由于功率级频率响应在两种不同的操作技术之间发生显着变化，因此转换器仅在其预测的运行环境中处于单一格式是相当有利的。

　　通过这种评估，采用了一个 n 沟道功率 MOSFET，并且正电压 VGS(ON) 由控制电路从栅极提供给 Q1 的源极端，以打开 FET。使用 n 沟道 FET 的好处是它的 RDS(on) 较低，但控制电路很棘手，因为需要暂停驱动。对于相同的封装尺寸，p 沟道 FET 具有更高的 RDS(on)，但通常可能不需要浮动驱动电路。

　　晶体管 Q1 和二极管 CR1 在虚线轮廓内示出，端子标记为 a、p 和 c。降压-升压功率级建模部分对此进行了详细讨论。

　　降压-升压稳态连续导通模式分析

　　以下是在连续导通方法中稳态运行的降压升压工作的描述。本部分的主要目标是推导连续导通模式降压-升压功率级的电压变换关系。

　　这将很重要，因为它表明了输出电压由占空比和输入电压确定的方式，或者相反，占空比如何根据输入电压和输出电压确定。

　　稳态意味着输入电压、输出电压、输出负载电流和占空比是恒定的，而不是变化的。大写字母通常提供给变量标签以表示稳态量级。在连续导通模式下，降压-升压转换器在每个开关周期采用几个状态。

　　ON 状态是每次 Q1 为 ON 且 CR1 为 OFF 时。关闭状态是每次 Q1 关闭且 CR1 开启时。一个简单的线性电路可以象征两种状态中的每一种，其中电路中的开关在每个状态的过程中被它们的匹配电路代替。图 2 显示了这两种情况的电路图。

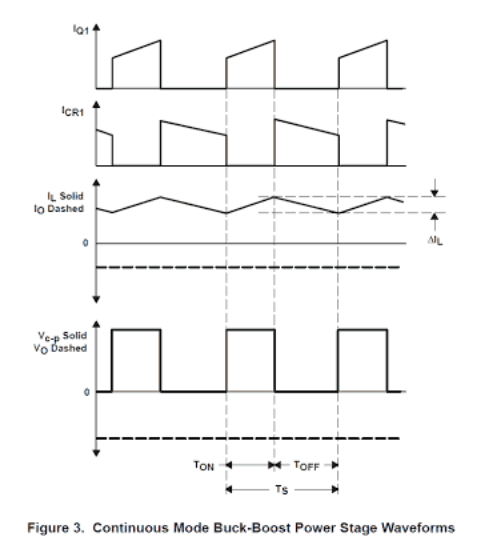
　　导通条件的周期为 D × TS = TON其中 D 是占空比，由驱动电路固定，以开关导通周期与单个完整开关序列周期 Ts 之比的形式表示。

　　OFF 状态的长度称为 TOFF。因为对于连续导通模式，每个开关周期只能找到几个条件，所以 TOFF 等于 (1−D) × TS。幅度 (1−D) 有时称为 D'。这些周期与图 3 中的波形一起呈现。

　　如图 2 所示，在导通状态期间，Q1 从漏极到源极的电阻 RDS(on) 降低，并表现出 VDS=IL× RDS(on) 的较小电压降。

　　此外，电感器的直流电阻上有一点电压降，等于 IL × RL。

　　因此，输入电压 VI 减去缺陷 (VDS IL× RL) 被置于电感 L 两端。CR1 在此期间关闭，因为它会被反向偏置。

　　电感电流 IL从输入电源 VI经 Q1 流向地。在导通状态过程中，电感两端的电压是恒定的，与 VI- VDS- IL× RL相同。

　　这个幅值 ΔIL( ) 被称为电感纹波电流。进一步观察，在此时间间隔内，输出负载电流的每一位都由输出电容器 C 进入。

　　因此，由于在电感器 L 中运行的电流无法立即调整，电流从 Q1 切换到 CR1。由于电感电流减小，电感两端的电压会反转极性，直到整流器 CR1 变为正向偏置并打开。

　　L 两端连接的电压变为 (VO- Vd- IL× RL)，其中幅度 Vd是 CR1 的正向电压降。此时，电感电流 IL从输出电容和负载电阻装置通过 CR1 流向负线。

　　观察到 CR1 与电感中电流循环路径的对齐，表明在输出电容和负载电阻组中运行的电流导致 VO为负电压。在关断状态的过程中，连接在电感两端的电压是稳定的，与（VO- Vd- IL× RL）相同。

　　保持我们同样的极性约定，这个连接的电压是负的（或在导通时间的过程中与连接的电压极性相反），因为输出电压 VO是负的。

　　因此，电感器电流在整个关断时间内降低。此外，由于连接电压基本稳定，电感电流线性减小。图 3 概述了 TOFF 过程中电感电流的降低。

　　这个幅值 ΔIL(-) 可以称为电感纹波电流。在稳定状态情况下，在开启时间过程中的电流上升 ΔIL( ) 和通过关闭时间的电流减小 ΔIL(-) 必须相同。

　　否则，电感器电流可能会从一个周期到另一个周期提供整体提升或降低，这将不是一个稳定的条件环境。

　　评估中发现的那样，这仅适用于连续传导模式。此时应进行必要的审查：

　　将 ΔIL 的两个值固定在彼此相等的位置，就等于使电感器上的伏秒趋于平稳。电感器上使用的伏秒是使用的电压和施加电压的周期的乘积。

　　对于常见的电路参数，这可能是估计未知幅度的最有效方法，例如 VO 或 D，并且这种方法将在本文中经常使用。电感上的伏秒稳定是一个自然要求，至少应该被视为欧姆定律。

　　在上述 ΔIL( ) 和 ΔIL(-) 等式中，输出电压隐含地假定在整个 ON 时间和 OFF 期间没有任何 AC 纹波电压是一致的。

　　这是一种公认​​的简化，需要几个单独的结果。首先，输出电容器被认为足够大，以至于其电压转换最小。

　　其次，电容器 ESR 的电压也被认为是最小的。这样的假设是合理的，因为交流纹波电压肯定会明显低于输出电压的直流部分。

　　V O的上述电压变化证明了可以通过微调占空比 D 来调整VO的事实。

　　描绘电路操作的一种不太复杂的定性方法是将电感器视为电力存储部件。每次 Q1 导通时，能量都会流过电感器。

　　当 Q1 关闭时，电感器将其部分能量提供给输出电容器和负载。通过建立 Q1 的导通时间来调节输出电压。例如，通过提高 Q1 的导通时间，可以放大发送到电感器的功率量。

　　在 Q1 的关断期间，额外的能量随后被发送到输出端，导致输出电压增加。与降压功率级相比，电感电流的典型幅度与输出电流不同。

　　要将电感电流与输出电流相关联，请查看图 2 和 3，观察仅在功率级关闭状态下流向输出的电感电流。

　　该电流在整个开关序列上的平均电流与输出电流相同，因为输出电容器中的近似电流应该等于零。

　　另一个重要观点是典型电感电流与输出电流成正比，并且由于电感纹波电流 ΔIL 与输出负载电流无关，电感电流的最小值和最大值精确地遵循平均电感电流。

　　例如，如果平均电感器电流由于负载电流降低而下降 2A，则在这种情况下，电感器电流的最低和最高值会降低 2A（考虑到保持连续导通模式）。

　　上述评估是针对连续电感电流模式下的降压-升压功率级功能。以下部分解释了不连续传导模式下的稳态功能。主要结果是推导非连续导通模式降压-升压功率级的电压转换关系。

　　降压-升压稳态不连续导通模式评估

　　在这一点上，我们检查负载电流减小和传导模式从连续转变为不连续时会发生什么。

　　请记住，对于连续导通模式，平均电感电流落后于输出电流，即在输出电流减小的情况下，平均电感电流也会减小。

　　此外，电感电流的最低和最高峰值精确地追求平均电感电流。如果输出负载电流降低到低于基波电流水平，则电感电流将在部分开关序列中为零。

　　这从图 3 所示的波形中可以明显看出，因为纹波电流的峰峰值水平无法随输出负载电流而改变。

　　在降压-升压功率级中，如果电感电流试图降至零以下，它会在零处停止（因为 CR1 中的电流单向移动）并一直持续到随后的开关动作开始。这种工作模式称为不连续导通模式。

　　降压升压电路在不连续导通格式下工作的功率级在每个开关周期中具有三种不同的状态，而连续导通格式则具有两种状态。

　　图 4 显示了功率级处于连续和不连续设置之间的外围的电感器电流状态。

　　在这种情况下，电感器电流简单地下降到零，而随后的开关周期在电流达到零之后开始。注意 IO 和 IO(Crit) 的值在图 4 中列出，因为 IO 和 IL 包含相反的极性。

　　要开始推导不连续导通模式降压-升压功率级电压转换比，请记住转换器通过不连续导通模式功能考虑的三种不同状态。

　　ON 状态是当 Q1 为 ON 且 CR1 为 OFF 时。关闭状态是当 Q1 关闭且 CR1 开启时。IDLE 条件是当每个 Q1 和 CR1 都关闭时。最初的两个条件与连续模式情况非常相似，除了 TOFF ≠ (1-D) × TS 之外，图 2 中的电路也是相关的。其余的切换序列是空闲状态。

　　此外，输出电感的直流电阻、输出二极管的正向压降以及功率 MOSFET 的导通状态压降通常被认为是微不足道的。

　　导通状态的时间周期为 TON = D × TS 其中 D 是占空比，由控制电路固定，表示为导通时间与一个完整开关序列的时间 Ts 的比率。OFF 状态的长度为 TOFF = D2 × TS。IDLE 周期是开关模式的其余部分，表示为 TS - TON - TOFF = D3 × TS。

　　对于连续导通模式，电压转换连接仅受输入电压和占空比的影响。在传统应用中，升降压功率级在连续导通模式或非连续导通模式之间进行选择。对于特定用途，选择一种传导模式，而使功率级维持相同的模式。