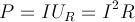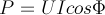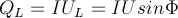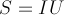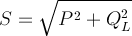电功率的计算公式及各功率间的关系

有关电功率的计算公式及各功率间的关系，交流电路中有功功率p、无功功率q和视在功率s之间的数量关系，也满足勾股定律，电阻电感交流电有功功率公式，无功功率公式，功率三角形得视在功率公式等。

电功率的计算公式

将电压三角形的每边乘以i就得到了如下右图所示的功率三角形，它表明了争先交流电路中有功功率p、无功功率q和视在功率s之间的数量关系，也满足勾股定律。

在r、l串联（即电阻和电感）交流电路中，只有r是耗能元件，故而电路的有功功率为：

由电压三角形可知，uc=ucosφ，所有，有功功率一般表示为：

上述公式中cosφ称为电路的功率因素，它是表征交流电路工作状态的重要技术数据之一。

电感l只与电源交换能量，其无功功率为：

在上述两个公式中，乘积iu是电源供给电路的总功率，虽然ui具有功率的形式，但并不是电路中真正消耗的功率，它包含着有功功率和无功功率两部分。只有有功功率才是电路实际消耗的功率。所以乘积ui称为视在功率，用字母“s”表示，视在功率的单位为伏安（va），或千伏安（kva）：定义式为：

由上右图所示功率三角形为一直角三角形，根据勾股定律：

由于纯电感只消耗无功功率，而电阻性负载消耗有功功率，所以在电感性负载交流电路中，衡量电能被利用来作有功功率的程度用功率因素cosφ来表示。

从有功功率p=uicosφ的公式中，可以看出，在同样的视在功率ui情况下，φ越小，cosφ越大，p越大，电源所做的有功功率越多，电能利用程度就越高。

电灯是电阻性负载，功率因素最高，φ为零，cosφ=1.电动机的功率因素在满载时为0.7~0.8，轻载时更低，为了充分利用发电和变电设备的能力，提高功率因素是有重大意义的。