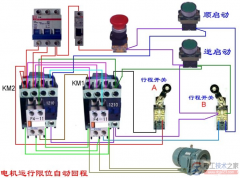
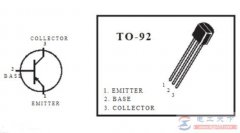
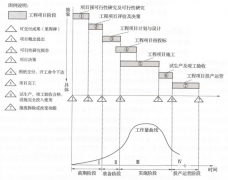
电容电压的关系,电容电压的计算公式
|
电容电压的关系,电容电压的计算公式 电容(Capacitance)亦称作“电容量”,是指在给定电位差下的电荷储藏量,记为C,国际单位是法拉(F)。 一般来说,电荷在电场中会受力而移动,当导体之间有了介质,则阻碍了电荷移动而使得电荷累积在导体上,造成电荷的累积储存,储存的电荷量则称为电容。 电容是指容纳电场的能力。 任何静电场都是由许多个电容组成,有静电场就有电容,电容是用静电场描述的。一般认为:孤立导体与无穷远处构成电容,导体接地等效于接到无穷远处,并与大地连接成整体。 电容(或称电容量)是表现电容器容纳电荷本领的物理量。 电容从物理学上讲,它是一种静态电荷存储介质,可能电荷会永久存在,这是它的特征,它的用途较广,它是电子、电力领域中不可缺少的电子元件。主要用于电源滤波、信号滤波、信号耦合、谐振、滤波、补偿、充放电、储能、隔直流等电路中。 电容器所带电量Q与电容器两极间的电压U的比值,叫电容器的电容。【电容电压的关系,电容电压的计算公式】 在电路学里,给定电势差,电容器储存电荷的能力,称为电容(capacitance),标记为C。 采用国际单位制,电容的单位是法拉第(farad),标记为F。电工天下 由于法拉这个单位太大,所以常用的电容单位有毫法(mF)、微法(μF)、纳法(nF)和皮法(pF)等,如果用GSC单位制,电容的单位是静法。 根据电容的定义,电容器两极间的单位电压下储藏的电量叫做电容,电容应该是电量与电压的比值,也就是C=Q/U。 一个电容器,如果带1库仑的电量时两级间的电压是1伏特,这个电容器的电容就是1法拉第,即:C=Q/U 。 但电容的大小不是由Q(带电量)或U(电压)决定的,即电容的决定式为:C=εS/4πkd 。其中,ε是希腊字母,读作epsilon,是一个常数,S为电容极板的正对面积,d为电容极板的距离,k则是静电力常量。常见的平行板电容器,电容为C=εS/d(ε为极板间介质的介电常数,S为极板面积,d为极板间的距离)。 电容的充放电计算公式 电容充放电时间的计算: 1.L、 元件称为“惯性元件”, C 即电感中的电流、 电容器两端的电压, 都有一定的“电惯性”, 不能突然变化。 充放电时间,不光与 L、C 的容量有关,还与充/放电电路中的电阻 R 有关。 “1UF 电容它的充放电时间是多长?”,不讲电阻,就不能回答。 2. 设 V0 为电容上的初始电压值; V1 为电容最终可充到或放到的电压值; Vt 为 t 时刻电容上的电压值。 例如,电压为 E 的电池通过 R 向初值为 0 的电容 C 充电,V0=0,V1=E,故充到 t 时刻电容 上的电压为: Vt=E × [1-exp(-t/RC)] 再如,初始电压为 E 的电容 C 通过 R 放电 , V0=E,V1=0,故放到 t 时刻电容上的电压为: Vt=E × exp(-t/RC) 又如,初值为 1/3Vcc 的电容 C 通过 R 充电,充电终值为 Vcc,问充到 2/3Vcc 需要的时间 是多少? V0=Vcc/3,V1=Vcc,Vt=2*Vcc/3,故 t=RC × Ln[(1-1/3)/(1-2/3)]=RC × Ln2 =0.693RC 注:以上 exp()表示以 e 为底的指数函数;Ln()是 e 为底的对数函数 3. 提供一个恒流充放电的常用公式:?Vc=I*?t/C. 【电容电压的关系,电容电压的计算公式】 关于用于延时的电容用怎么样的电容比较好,不能一概而论,具体情况具体分析。实际电容 附加有并联绝缘电阻,串联引线电感和引线电阻。还有更复杂的模式--引起吸附效应等等。 E 是一个电压源的幅度, 通过一个开关的闭合, 形成一个阶跃信号并通过电阻 R 对电容 C 进行充电。E 也可以是一个幅度从 0V 低电平变化到高电平幅度的连续脉冲信号的高电平幅度。 电容两端电压 Vc 随时间的变化规律为充电公式 Vc=E(1-e-(t/R*C))。 其中的: -(t/R*C) 是 e 的负指数项,这里没能表现出来,需要特别注意。式中的 t 是时间变量,小 e 是自然指 数项。举例来说:当 t=0 时,e 的 0 次方为 1,算出 Vc 等于 0V。符合电容两端电压不能突 变的规律。 对于恒流充放电的常用公式:?Vc=I*?t/C,其出自公式:Vc=Q/C=I*t/C。 电工天下 举例:设 C=1000uF,I 为 1A 电流幅度的恒流源(即:其输出幅度不随输出电压变化)给电容 充电或放电,根据公式可看出,电容电压随时间线性增加或减少,很多三角波或锯齿波就是 这样产生的。根据所设数值与公式可以算出,电容电压的变化速率为 1V/mS。 这表示可以 用 5mS 的时间获得 5V 的电容电压变化;换句话说,已知 Vc 变化了 2V,可推算出,经历 了 2mS 的时间历程。 当然在这个关系式中的 C 和 I 也都可以是变量或参考量。详细情况可 参考相关的教材看看。供参考。 4. 可得: 首先设电容器极板在 t 时刻的电荷量为 q,极板间的电压为 u.,根据回路电压方程:U-u=IR(I 表示电流),又因为 u=q/C,I=dq/dt(这儿的 d 表示微分哦),代入后得到: U-q/C=R*dq/dt, 也就是 Rdq/(U-q/C)=dt,然后两边求不定积分, 并利用初始条件: t=0,q=0 就得到 q=CU 【1-e^ -t/(RC)】这就是电容器极板上的电荷随时间 t 的变化关系函数。 顺便指出,电工学上常把 RC 称为时间常数。 相应地,利用 u=q/C,立即得到极板电压随时间变化的函数, u=U【1-e^ -t/(RC)】。 从得到的公式看,只有当时间 t 趋向无穷大时,极板上的电荷和电压 才达到稳定,充电才算结束。 但在实际问题中,由于 1-e ^-t/(RC)很快趋向 1,故经过很短的一段时间后,电容器极板间电荷和电压的变化已经微乎其微,即使用灵敏度很高的电学仪器也察觉不出来 q 和 u 在微小地变化,所以这时可以认为已达到平衡,充电结束。 举例,假定 U=10 伏,C=1 皮法,R=100 欧,利用推导的公式可以算出,经过 t=4.6*10^(-10)秒后,极板电压已经达到了 9.9 伏。 |