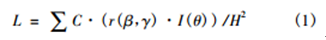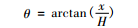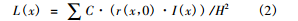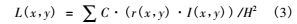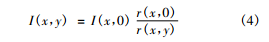工程师笑了：有了这个863成果 LED路灯亮度计算变得如此简单

　　2016年4月，《照明工程学报》第27卷第2期刊登了《直线道路的r(x，y)反射表和亮度计算》的技术论文。文章介绍的计算方法是国家863计划--“十城万盏”半导体照明应用研究及示范--“标准化、模块化 LED道路照明及智能控制系统研发及示范”的研究成果。

　　文章通过引入新的基于直角坐标系的路面反射表，即r(x，y)表，大大简化了道路亮度的计算过程，一举解决了LED路灯均匀性的难题。

　　关于该成果对于道路照明产业的重要意义，我们可以引用论文第一作者上海三思周士康在文章最后表达的五点来说明：

　　l)本文把CIE的反射表r(β，γ)改造成直角坐标下的r(x，y)表，结果和路面坐标一致，这一改造的效果使得道路亮度计算十分便利。

　　2) 某些亮度分布可以用商用软件来进行，但商用软件局限性较大，没有数字结果，也不能根据用户需求而变化。相对于商用软件，本文对亮度的分析更为形象、系统和深入，还可以得到更实用的图形化的结果，而且本文的量化计算方法是普通设计人员部不难掌握的。

　　3) 本文的前提是直线道路，但由于实际上绝大多数道路都是直线的，因此本文的结果的应用范围非常广。

　　4)对不同的灯高，应该有不同的r(x，y) 表，但实际上灯具的高度只有有限的几种，如8m、lOm，由于本文的方法是一般光学，工程设计人员都易于掌握的，可以用编程来更简化计算过程，因此这也没有对设计带来很大的影响。

　　计算道路的亮度变得容易了，这样就可以方便地修改 LED的光强分布从而得到设计者要求的亮度分布。而有了光强分布则可以通过文献 [9] 的方法计算透镜的形状。这将大大加快等亮度分布的照明灯具的设计进程。这将是更为重要的应用，但有关内容已不在本文的范畴之内。

　　下面，小编就将这篇文章全文分享出来，希望能对从事LED路灯研发的朋友有所帮助。

　　注：为了获得更好的阅读体验，建议您在电脑上阅读文章。方法：点击右上角--分享到手机QQ--我的电脑，同时保持电脑QQ在线，即可发送文章链接到电脑QQ上。

　　全文如下：

　　直线道路的 r ( x，y)反射表和亮度计算

　　周士康，陈春根，许礼，王鹰华

　　( 上海三思科技发展有限公司，上海201100)

　　摘要：亮度评价方法在道路照明评价中变得越来越重要，但有关亮度的计算工作却十分缺乏。虽然用 CIE(国际照明委员会)提供的路面反射表r(β，γ) 可以计算道路的亮度分布，但其实际的计算过程却很困难。分析其因难的根本原因是在于道路亮度分布是基于直角坐标而 CIE的反射表却基于球坐标。本文引入了一个新的基于直角坐标的路面反射表，称为r(x，y)表。用r(x，y)表分析路面反射特性将更直观、形象面且更具有系统性，计算直线道路亮度分布也更容易。文章给出了 r(x，y)表的导人方法，详细分析了不同路面性质时在沿道路方向和垂直道路方向上的反射系数变化规律，以及用 r(x，y)表方便地计算单个车道和整个道路的亮度分布的方法。这将大大有利于分析给定灯具时道路的亮度如何分布，以及如何设计等亮度分布的灯具。

　　关键词：道路照明；路面反射表；r(x，y)表；道路亮度分布；CIE

　　引言：

　　在道路照明的评价方法中，亮度评价比照度评价更为恰当，特别是对于高速公路的照明更是如此。这是由于亮度依赖于司机的观察，它与道路交通事故是紧密相关的，而照度只依就仪器的测量。许多国家已经把亮度评价作为道路照明质量评价的主要方法[1-3] ，亮度的计算在道路照明中变得越来越重要了。

　　与传统灯具相比，LED可以比较容易地用各种透镜来改变其光强分布，因此 LED道路照明可以实现精确的光强分布，从而实现较高的道路照明亮度均匀性，而同时又能够满足一定的照度均匀性，以满足某些道路照明标准的要求。这种现实的可能性大大地增加了道路照明工程对首先满足均匀亮度分布而不是均匀照度分布的需求，这也提高了对 LED 灯具的道路照明亮度分布计算的要求。但由于其复杂性，这种计算在以前是技术上的弱项，关于照明亮度分布的分析还只能依赖于市售的照明软件，而这些软件的分析只能到有限的结果，而且是不能按设计者的要求进行分析。迄今为止道路照明方面亮度分布计算的文章还极少。本文的目标是改进道路亮度分布的计算方法，从而能更方便地设计等亮度分布的 LED透镜。

　　l 道路亮度分布计算的困难

　　道路的亮度与许多因素相关，包括不同的路面类型，光线的方向，观察者的位置，观察的方向等。为了使得亮度分布的计算规范化，CIE (国际照明委员会)和PIARC(国际道路会议常设协会)规定了标准路面和标准观察条件 [3-4]，这使得亮度计算有了标准。这样，在确定的点的亮度 L可以用下列公式来计算：

　　这里I (θ)是灯具光强度分布，H为灯具安装高度，求和则包括所有能射到该点的灯具，对确定道路来说 C是常数，由于本文只关心相对亮度，我们不必给定 C值。

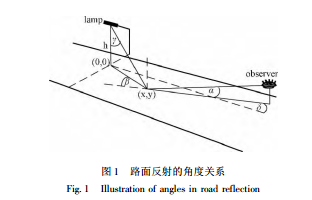
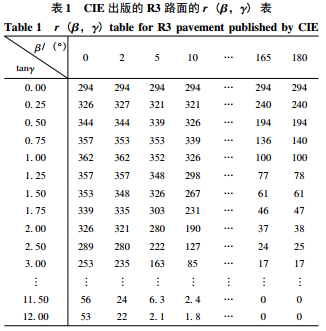
　　式(l)中的变量r称为简化反射系数，是β和γ的函数。按图1所示，β为入射面和观察面的夹角，γ是行具垂线和光线的央角。简化反射系数表也称为反射表，在此用r(β，γ) 表示，表l就是CIE出版的 R3路面为例的 r(β，γ)表[4-5]。

　　用CIE提供的r(β，γ)表就可以用式(l)来计算路面亮度了[2,3,8]。但是用r(β，γ)去计算通常是直角坐标下的道路时是很困难的。而且，考虑到 r(β，γ)给出的只是道路某一个点由一个灯具引起的亮度贡献，一个车道的亮度分布还必须考意每一个观察点上各灯的贡献之和，加之道路还不止一个车道，可以想象计算将十分困难。计算的复杂性也是很少有亮度计算的文章出现的原因。

　　2 计算道路亮度分布的新方法

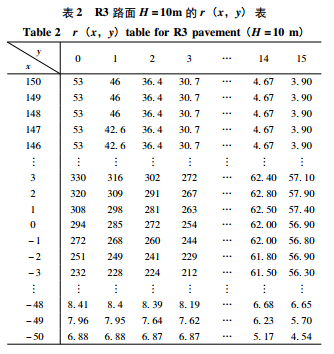
　　分析其计算复杂性的基本原因其实还在于角度关系在直角坐标下的不方便计算，本文首次提出这一个问题在直线道路中是可以解决的。我们下面将证明，在直线道路上所有的灯有相同的高度，相同的灯间距，相同的光强分布的条件下，可以引入一个新的只依赖于坐标 x和 y而不是β和γ的反射系数。这一新的 r(x，y)表将在第3节中给出其导入方法，在此先提前将结果给出，表2就是 R3路面和10m灯高为例的r(x，y)表。

　　表2的坐标原点位于灯具的正下方，x方向指向沿道路的方向，y方向则垂直于道路。考虑到前向的反射系数要大于后向的，表2中沿道路的x 方向取值范围是向后50m向前150m，而垂直于道路的 y方向取值范围在0-12m。

　　这样，对于直线道路上固定灯高的道路亮度，只需简単的算术运算就可以得到亮度分布了。读者可以用第3节的方法导入他们自己的不同灯高的r(x，y)表，并用它进行进一步的计算。

　　3 反射系数r(x，y)表的导入方法

　　为了在处理中不损失精度，我们首先对r(β，γ)表进行内插处理，用五个节点的线性内插就可以保证精度。这样就得到了一个有小步长的更为精确的r(β，γ)表。然而，此表还是以β和γ为自变量，并非我们所希望的表，具体结果不在此给出了。

　　然后，给出一个r(x，y) “空”表，其x和y 的范围及步长就如前面我们在表 2 中给出的那样。由于此时，路面类型、灯的高度、灯的间距都是已知，表2中每格的x 和y值也都固定，因此每点的β和γ也已知，不需要额外的计算就可以由内插后的r(β，γ)中的反射系数得到在r(x，y)点的反射系数。由于内插后的r(β，γ)比原来的，r(β，γ) 表精度高，因此得到的r(x，y)表也有足够的精度。这一过程也是一个繁琐的工作，然而这是一个一劳永逸的工作，路面的类型和灯具的高度都是有限的几种，因此，需要计算的r(x，y)也是有限的几个。我们不必要在此给出详细的计算过程，而只是在表2中给出对 R3路面l0m灯高的计算结果。

　　必须说明，CIE 给出的 r ( β，γ) 表是权威的原始数据，是由实际测量得到的标准数据。新的r( x，y) 表是用此原始数据对直线道路进行了处理，但是这种处理不仅仅是数学上的坐标变换，实际上新的 r ( x，y) 表的引入带来了意想不到的好处，以下可以看到，它使得分析道路反射特性十分方便，而且计算更为简便和直观。

　　4 由r(x，y)表分析路面特性

　　4.1 R3路面的r(x，y)表的3D总图

　　因为r(x，y)表是在笛卡尔系统中的，这使得我们可以比较容易的画出 r(x，y)的3D图，而这在以前是比较困难的事。图2给出了 R3路面r(x，y)表的3D图形。图中的x 和y就是道路的坐标，从图中可以清楚地看到直线道路的反射系数分布。这一个图包含了道路的整个反射性质，这是令人兴奋的结果，也初步看到了引入r(x，y)表的优越性。

　　4.2 R3路面 y=0车道的反射系数

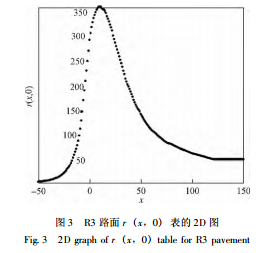
　　图3显示 R3路面 y=0处的反射系数。事实上图3是图2的一条线，但它包含计算y=0那个车道上亮度分布所需要的所有数据。图3中曲线的峰值不在 y=0而是位于 x=12附近。而且曲线向右衰减得快，向左衰减得慢。这表示对同样的灯具同样的距离时，前向光(x＞0的灯发出的光)比后向光(x＜0的灯发出的光)反射得更多。这也意味着计算道路亮度分布时，相对后方的灯而言，前方较远处的灯也有贡献。对 R3路面30m的灯间距，由 5.2 节的分析知道. 计算路面某点的亮度时，一般取前向4个灯后向l个灯即可。

　　在 y ＞ 0 的其他车道上，与图 3 相比，曲线的数值不同但其趋向类似。

　　4. 3反射系数和路面材料的关系

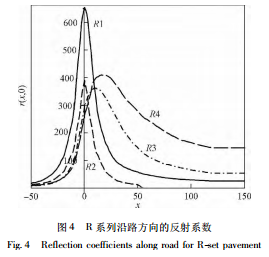
　　不同材料路面的 r ( x，y)表可以按照第 2 节的方法得到。例如对 R 系列的路面包含四个路面类型：R1，R2，R3 和 R4。图 4 表示了 R 系列的四种路面的 r ( x，0) 的变化情况。

　　从图 4 我们可以得到有价值的结论，即路面材料对反射系数影响非常大，R1 和 R2 类路面的方向性不强 ( 前向和后向光的反射差别不大) ，而 R3 或R4 路面有很强的方向性。

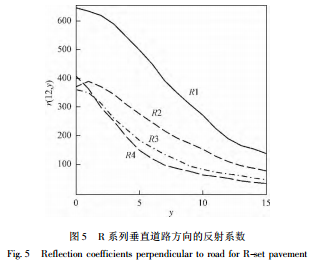
　　有了 r ( x，y) 表后，垂直于道路方向上反射系数的变化规律也易于得到。图 5 给出了 R 路面系列在垂直于道路方向上 r ( 12，y) 的变化规律。四条曲线随 y 的变化趋势类似，但 R1 的数值较大，这给垂直于道路方向上的亮度分析提供了基础。

　　5 用 r ( x，y) 表计算亮度分布

　　5.1 单灯光强分布

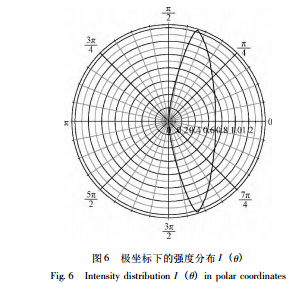
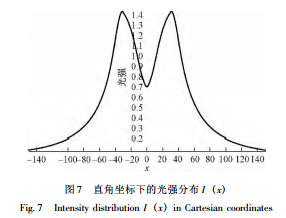
　　用r ( x，y) 表可以使得直线道路上的亮度分布的计算大大简化。先考虑一个车道上的亮度分布。图6 给出了我们设计的一个灯具极坐标下的 I ( θ) 分布的例子，不难给出 I ( θ) 的数学表达式，它可以由图形模拟得到，也可以由描述灯具光强分布的IES 文件得到，在此我们将不给出其具体数学表达式。有了 I ( θ) 分布，就可以用式 ( 1) 计算亮度分布。

　　极坐标中的 I ( θ)很容易改为直角坐标下的I( x) ，这两个自变量的关系是：

　　10m 灯高时直角坐标下 I ( x)的图形显示见图 7。

　　5. 2 单车道亮度分布

　　由于亮度是正比于反射系数和光强的乘积，即路面上亮度为 r ( x，0) I ( x) ，即：

　　用图表示这个乘积就是图 8 的曲线，实际上图8 就是图 3 和图 7 相乘的结果。这就是单个灯具在单车道上的亮度分布。这里约定坐标 x 为灯具离开观察点的距离。由图可以看到前向光 ( x ＞ 0) 的贡献明显大于后向光 ( x ＜ 0 )。这是一个由于引入 r ( x，y) 表而轻易得到的一个灯具在直线道路上引起的亮度是如何分布的，这是十分有价值的结果，下面我们将看到，有了它我们就不难得到所有灯在路面所有点的亮度分布了。

　　设灯间距为 30m，则由图 8 可以估算得正向第4 个灯 ( 120m 远) 对观察点的亮度贡献只是最大贡献的 2% ，若灯间距缩小为 25m，则第 4 个灯的贡献也只有最大贡献的 3%。这样我们可以得到在道路亮度计算中的重要结论： 只需考虑正向 4 个灯方向 1 个灯就有足够的精度了。考虑到 R3 路面是反射方向性较强的路面，而且 y ≠0 处的反射系数更小，因此，可以放心地把这一结论用在其他路面和其他车道其他灯间距。

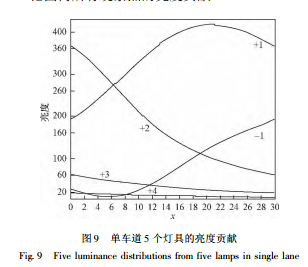
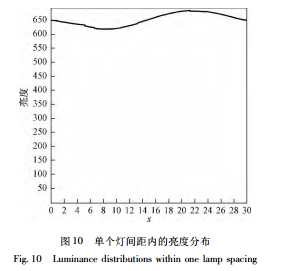
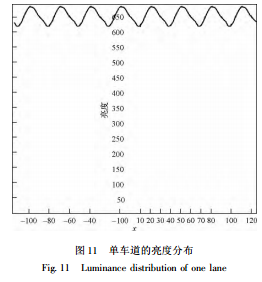
　　对于一个较长的直线道路，每两个灯具间的亮度分布都是相同的，我们只需考虑一个灯间距的范围就可以了，上面已经说明，在每个点只需考虑 5个灯具。现在我们有了图 8，就可以更清楚用图形来表现这 5 个灯具影响的规律。以灯间距为 30m 为例，在图 9 中分别给出了这 5 个灯在两个灯具间即30m 范围内所有观察点的亮度贡献。

　　把图 9 中的 5 条线相加就是一个灯间距间的亮度分布了，结果显示在图 10 中。图中显示此灯具单车道的亮度均匀性约为 91%。

　　整个车道约 240m 范围内的亮度分布见图 11，其实图 11 就是图 10 的 8 次周期性重复。在图 11 中可以看到亮度周期性的波动，这种波动是间距式灯具照明不可避免的，但图中 10% 的波动是比较小的。如果有严重的波动，就会形成影响交通安全的所谓 “斑马线”，而这种斑马线是可以在灯具设计时计算出来得到数字的结果，用于进一步分析，具体方法就不在本文中描述了。

　　可见，有了直角坐标下的反射表 r ( x，y) ，我们就可以得到如图 8 所示的单灯在单车道上的亮度分布。再把此分布分成 5 段，我们就得到了如图 9所示的 5 个有贡献的灯具在一个点间距内的亮度。把此 5 条曲线相加就得到了如图 10 所示的一个灯间距内单车道的亮度分布，它就是整个车道的亮度分布。以上这一图形化表现的过程清晰连贯，脱离了球坐标下由 r ( β，γ) 表计算的复杂性，是引入 r( x，y)表的另一个重要应用。

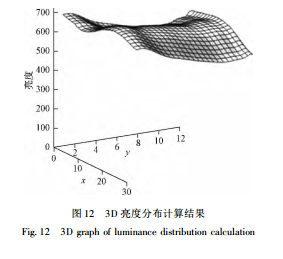
　　5. 3整个道路的亮度分布

　　I ( θ) 和 I ( x) 描述的是单车道的强度，对多车道的道路，灯具的光强分布可改为用两个自变量的函数 I ( x，y)。这样式 ( 2)应改成式 ( 3) ：

　　如何得到 I ( x，y) 呢? 我们已经有了垂直于路面的反射系数分布，R3 路面的结果见图 5。我们可以用此分布来作为由 I ( x) 扩展为 I ( x，y) 的依据。简单地说，由于 r ( x，y) 比 r ( x，0) 小，如果希望道路的亮度 L 在整个道路上都均匀，只有I ( x，y) 比 I ( x，0) 大才行。作为初级近似，我们可以用式 ( 4) 求得 I ( x，y) ：

　　这样，就可以把上面单车道的亮度计算结果扩展到多车道。用简单的程序不难计算得到整个道路上的亮度分布。仍然以 R3 路面为例，结果显示在图 12 中，在此例中整个亮度均匀性约为 85%。

　　6 讨论

　　1) 本文把 CIE 的反射表 r ( β，γ) 改造成直角坐标下的 r ( x，y) 表，结果和路面坐标一致，这一改造的效果使得道路亮度计算十分便利。

　　2) 某些亮度分布可以用商用软件来进行，但商用软件局限性较大，没有数字结果，也不能根据用户需求而变化。相对于商用软件，本文对亮度的分析更为形象、系统和深入，还可以得到更实用的图形化的结果，而且本文的量化计算方法是普通设计人员都不难掌握的。

　　3) 本文的前提是直线道路，但由于实际上绝大多数道路都是直线的，因此本文的结果的应用范围非常广。

　　4) 对不同的灯高，应该有不同的 r ( x，y ) 表，但实际上灯具的高度只有有限的几种，如 8m、10m，由于本文的方法是一般光学工程设计人员都易于掌握的，可以用编程来更简化计算过程，因此这也没有对设计带来很大的影响。

　　5) 计算道路的亮度变得容易了，这样就可以方便地修改 LED 的光强分布从而得到设计者要求的亮度分布。而有了光强分布则可以通过文献 ［9］的方法计算透镜的形状。这将大大加快等亮度分布的照明灯具的设计进程。这将是更为重要的应用，但有关内容已不在本文的范畴之内。

　　参考文献

　　［1 ］ ANSI．American National Standard Practice of Roadway Lighting． ANSI / IESNA RP － 8 － 00，2005．

　　［2 ］ MOHURD．Standard for Lighting Design of Urban Road：CJJ 45-2006．

　　［3 ］ CIE．Lighting of Road for Moto and Pedestrian Traffic，CIE publication N0. 115，2008．

　　［4 ］ CIE．Road Surfaces and Lighting．CIEpublicationN0.66，1984．

　　［5 ］ CIE．RoadSurfaceandRoadMarkingReflection Characteristics．CIE publication No．144，2001．

　　［6 ］ BSEN 13201-3 Road Lighting Part3 Calculation of performance． 2003．

　　［7 ］ FENGZexin，LUO Yi，HAN Yanjun．Design of LEDfreeformopticalsystem for road lighting with high luminance /illuminanceratio．Opt．Express，2010，18( 21) ： 22020-22031．

　　［8 ］ CIE．Calculation andMeasurementofLuminanceand Illuminance in Road Lighting．CIEpublicationN0.30-2，1982．

　　［9 ］ 周士康，陈春根，许礼，等．光通量线方法用于 LED二次 光 学 设 计 ［J］．照 明 工 程 学 报，2016，27( 1) ： 101．