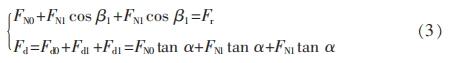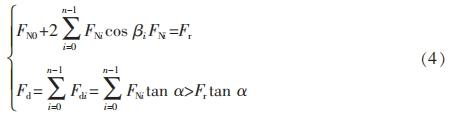成对安装时“防松”轴承和“紧压”轴承的轴向力到底如何确定？

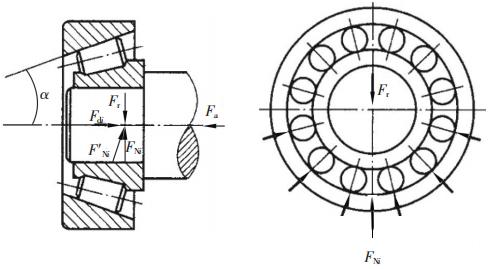
角接触球轴承和圆锥滚子轴承派生轴向力分析

角接触球轴承和圆锥滚子轴承由于存在接触角，会产生派生轴向力。以图1所示圆锥滚子轴承为例，由于滚动体与滚道的接触线与轴线之间存在接触角α，当受到径向载荷Fr作用时，各滚动体的反力FNi′并不指向轴承半径方向，而是可以分解为一个径向分力FNi和一个轴向分力Fdi（如图1a）。各滚子径向分力FNi沿半径方向指向中心（如图1b），各轴向分力Fdi沿轴向分布。当受载滚动体数量不同时，各滚动体径向分力与轴向分力也随之变化。

图1 圆锥滚子轴承受力图

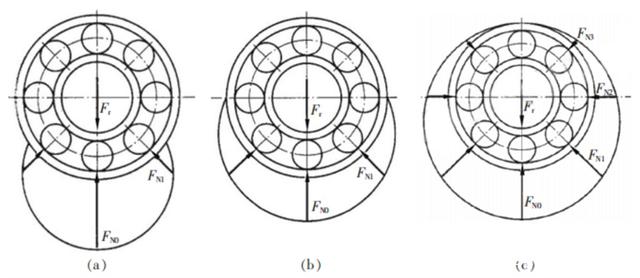
图2 轴承滚动体径向分力

如图2所示，设轴承各滚动体沿中心垂线对称均匀分布：最下方滚动体编号为0，与外载荷Fr夹角为0；最下方滚动体左右两侧的滚子编号为1，与外载荷Fr夹角为β1；沿两侧依次向上，编号为2的滚子与外载荷Fr夹角为β2，编号为i的滚子与外载荷Fr夹角为βi。当只有最下方一个滚动体受载时有：

当受载的滚动体数目增多时，各个滚动体的受载情况可类比只有一个滚动体受载的情况。设各滚动体所受径向分力依次为FN0，FN1，…，FNi，轴向分力依次为Fd0，Fd1，…，Fdi，且：

FN0，FN1，…，FNi在垂直方向的分力之和与外载荷Fr相平衡，水平方向的分力相互抵消；Fd0，Fd1，…，Fdi之和构成派生轴向力Fd。例如图2a中，当3个滚动体受载时满足：

此时派生轴向力Fd不再等于Frtanα，而是大于Frtanα。 推广到受载滚动体数目为n时，力平衡条件为：

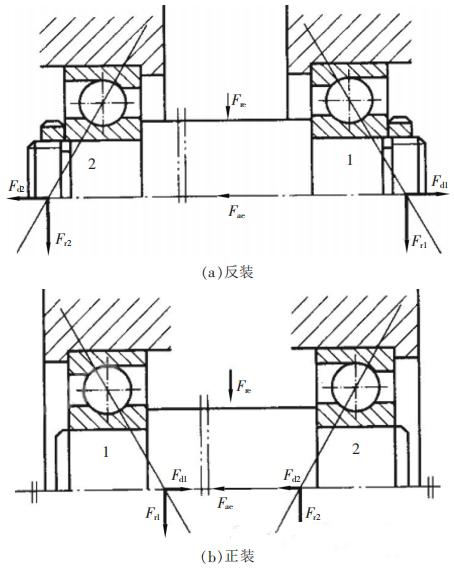
式中：n———受载滚动体数目；

Fdi———各滚动体上派生的轴向力；

FNi———各滚动体上的径向分力。

由上述析可以看出，受载滚动体数目越多，则每个滚子所受载荷越均匀，同时轴承的派生轴向力也越大。对于同一个轴承（设α不变），在同样的径向载荷作用下，当轴向力Fa由最小值Frtanα（只有一个滚动体受载）逐渐增大时，同时受载的滚动体数目也随之逐渐增多，与轴向力Fa相平衡的派生轴向力Fd也随之增大。对于实际工作的角接触球轴承或圆锥滚子轴承，为保证受载均匀及可靠工作，应至少达到下半圈滚动体全部受载，因此在安装时要保证足够的轴向力，不能有较大的轴向窜动量。

角接触球轴承和圆锥滚子轴承实际轴向力分析

角接触球轴承和圆锥滚子轴承在使用时通常成对安装，可采用外圈宽边相对安装（反装，图3a）和外圈窄边相对安装（正装，图3b）两种方式，反装时两轴承派生轴向力方向相背，正装时两轴承派生轴向力方向相对。进行寿命计算时需要分析计算两个轴承的实际轴向力，如图3所示，设轴系所受外加径向外载荷为Fre，外加轴向载荷为Fae。这里将派生轴向力方向与外加轴向载荷Fae方向相同的轴承标为2，另一个轴承标为1，按照力平衡条件，可确定两轴承所受径向载荷Fr1和Fr2，进而求得两轴承的派生轴向力Fd1和Fd2。当轴向平衡时，应有Fae Fd2=Fd1，此时两轴承所受轴向力Fd1和Fd2就是自身的派生轴向力。

图3 圆锥滚子轴承轴向力分析图

若等式不成立时，会出现下面两种情况：

当Fae Fd2>Fd1时，轴系有向左窜动的趋势，则轴承1为限位轴承，被“压紧”，轴承2为非限位轴承，被“放松”。实际上轴系必须处于平衡位置，因此轴承座会通过轴承元件施加一个附加的轴向力（与Fd1同向）来阻止轴的窜动，所以被“压紧”的轴承1所受的总轴向力Fa1必须与Fae Fd2相平衡，即：Fa1=Fae Fd2；而被“放松”的轴承2只受其自身的派生轴向力，即：Fa2=Fd2。

当Fae Fd2d1时，同理，轴承1为非限位轴承，被“放松”，其所受轴向力为：Fa1=Fd1；轴承2为限位轴承，被“压紧”，其所受轴向力为Fa2=Fd1-Fae。

如果两轴承的标定方式变化，通过分析也可以得到相同的结论。

因此，计算角接触球轴承和圆锥滚子轴承所受实际轴向力时，先通过派生轴向力及外加轴向载荷的分析，判定限位轴承（被压紧）和非限位轴承（被放松），“被放松”轴承的实际轴向力仅为其本身派生轴向力，“被压紧”轴承的实际轴向力为除去其本身派生轴向力外其余轴向力的代数和。

总之

（1）角接触球轴承和圆锥滚子轴承在同样径向载荷作用下，适当增大轴向载荷，可使受载的滚动体数目会增多，保证轴承可靠工作。

（2）这类轴承使用时成对安装，可通过标定限位轴承和非限位轴承来计算的实际轴向力。